OghmaNano Simulate organic/Perovskite Solar Cells, OFETs, and OLEDs DOWNLOAD

1D/2D Drift–Diffusion Electrical Model – Overview

Figure 1: Simulating a JV curve from just below J_sc to above V_oc. Watch carriers flood the device as bias is applied. A key differentiator of OghmaNano (and essential for simulating organic devices) is its ability to resolve charge carriers in both energy and position space. This is vital for modelling devices with high trap densities in the time domain. Resolving traps in energy space also allows average mobility to vary dynamically with carrier density.

OghmaNano’s electrical model is a fully-coupled 1D/2D drift–diffusion solver designed for both crystalline and highly disordered semiconductors — including organics, perovskites, and amorphous silicon. While it shares the same core drift–diffusion framework as many other tools, it goes further by explicitly solving the Shockley–Read–Hall (SRH) trapping and recombination equations as a function of both energy and position.

This approach captures effects such as:

Mobility and recombination rates changing with carrier population.
Non-equilibrium occupation of trap states during fast transients (no assumption of quasi-equilibrium).
Accurate simulation of time-of-flight (ToF), CELIV, and other transient experiments.

When simulating ordered materials, trap states can simply be disabled for a standard crystalline semiconductor model.

Numerical Framework

The solver uses a finite-difference discretisation of the coupled drift–diffusion, continuity, and Poisson equations, solved self-consistently via Newton–Raphson iteration. Adaptive time-stepping is available for transient simulations, ensuring stability across fast and slow processes. Optical generation profiles from the built-in optical solvers (uniform, exponential decay, or full transfer matrix) can be coupled directly into the electrical simulation.

Energy Levels

In organics, the conduction and valence bands correspond to the LUMO and HOMO levels:

$$E_{LUMO} = -\chi - q\phi$$ $$E_{HOMO} = -\chi - E_g - q\phi$$

The internal electrostatic potential distribution is obtained by solving Poisson’s equation:

$$\nabla \cdot \epsilon_0 \epsilon_r \nabla \phi = q (n_{f} + n_{t} - p_{f} - p_{t} - N_{ad} + - N_{ion} + a)$$

where:

$n_{f}, p_{f}$ are free electron and hole densities.
$n_{t}, p_{t}$ are trapped electron and hole densities.
$N_{ad}$ is the doping density.
$N_{ion}$ is the background density of fixed ionic charge.
$a$ is the density of mobile ions (important for perovskite modelling).

Free Carrier Statistics

Free carriers can be treated using either:

Maxwell–Boltzmann statistics:

$$n_{l} = N_c \exp\left(\frac{F_n - E_{c}}{kT}\right)$$ $$p_{l} = N_v \exp\left(\frac{E_{v} - F_p}{kT}\right)$$

Fermi–Dirac statistics:

$$n_{free}(E_{f},T) = \int^{\infty}_{E_{min}} \rho(E) f(E,E_{f},T) \, dE$$ $$p_{free}(E_{f},T) = \int^{\infty}_{E_{min}} \rho(E) f(E,E_{f},T) \, dE$$

where:

$$f(E) = \frac{1}{1 + e^{(E-E_f)/kT}}$$

For Fermi–Dirac statistics, free carriers are assumed to move in a parabolic band:

$$\rho(E)_{3D} = \frac{\sqrt{E}}{4\pi^2} \left( \frac{2m^{*}}{\hbar^2} \right)^{3/2}$$

The average carrier energy is then:

$$\bar{W}(E_{f},T) = \frac{\int^{\infty}_{E_{min}} E \rho(E) f(E,E_{f},T) \, dE}{\int^{\infty}_{E_{min}} \rho(E) f(E,E_{f},T) \, dE}$$

Carrier trapping, de-trapping, and recombination

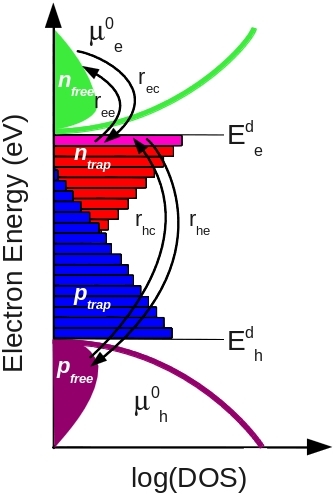Density of states in an Generic solar cell

Figure 2: A 0D energy slice through the model.

To describe charge becoming trapping into trap states and recombination associated with those states the model uses Shockley-Read-Hall (SRH) theory. A 0D depiction of this SRH recombination and trapping is shown in figure 2. The free electron and hole carrier distributions are labeled as $n_{free}$ and $p_{free}$ respectively. The trapped carrier populations are denoted with $n_{trap}$ and $p_{trap}$, they are depicted with filled red and blue boxes. SRH theory describes the rates at which electrons and holes become captured and escape from the carrier traps. If one considers a single electron trap, the change in population of this trap can be described by four carrier capture and escape rates as depicted in figure 2. The rate $r_{ec}$ describes the rate at which electrons become captured into the electron trap, $r_{ee}$ is the rate which electrons can escape from the trap back to the free electron population, $r_{hc}$ is the rate at which free holes get trapped and $r_{he}$ is the rate at which holes escape back to the free hole population. Recombination is described by holes becoming captured into electron space slice through our 1D traps. Analogous processes are also defined for the hole traps.

For each trap level the carrier balance

$$\frac{\delta n_t}{\partial t}=r_{ec}-r_{ee}-r_{hc}+r_{he}$$

is solved, giving each trap level an independent quasi-Fermi level. Each point in position space can be allocated between 10 and 160 independent trap states. The rates of each process $r_{ec}$, $r_{ee}$, $r_{hc}$, and $r_{he}$ are give in table 1 below. The escape probabilities are given by:

$$e_n=v_{th}\sigma_{n} N_{c} exp \left ( \frac{E_t-E_c}{kT}\right )$$

and

$$e_p=v_{th}\sigma_{p} N_{v} exp \left ( \frac{E_v-E_t}{kT}\right )$$

where $\sigma_{n,p}$ are the trap cross sections, $v_{th}$ is the thermal emission velocity of the carriers, and $N_{c,v}$ are the effective density of states for free electrons or holes. The distribution of trapped states (DoS) is defined between the mobility edges as

$$\rho^{e/h}(E)=N^{e/h}exp(E/E_{u}^{e/h})$$

Mechanism	Symbol	Description
Electron capture rate	$r_{ec}$	$n v_{th} \sigma_{n} N_{t}(1-f)$
Electron escape rate	$r_{ee}$	$e_{n} N_{t} f$
Hole capture rate	$r_{hc}$	$p v_{th} \sigma_{p} N_{t} f$
Hole escape rate	$r_{he}$	$e_{p} N_{t} (1-f)$

Table 1: SRH capture escape rates

where, $N_{e/h}$ is the density of trap states at the LUMO or HOMO band edge in states/eV and where $E_{U}^{e/h}$ is slope energy of the density of states. The value of $N_{t}$ for any given trap level is calculated by averaging the DoS function over the energy ($\Delta E$ ) which a trap occupies:

$$N_{t}(E)=\frac{\int^{E+\Delta E/2}_{E-\Delta E/2} \rho^{e}{E} dE}{\Delta E}$$

The occupation function is given by the equation,

$$f(E_{t},F_{t})=\frac{1}{e^{\frac{E_{t}-F_{t}}{kT}}+1}$$

Where, $E_{t}$ is the trap level, and $F_{t}$ is the Fermi-Level of the trap. The carrier escape rates for electrons and holes are given in table 1.

Free-to-free carrier recombination

Free-to-free recombination is described using equation

$$R_{free}=k_{r}(n_{f}p_{f}-n_{0}p_{0})$$

Auger recombination

Auger recombination is included in the model as

$$R^{AU}=(C^{AU}_{n}n+C^{AU}_{p}p)(np-n_{0}p_{0})$$

where $C^{AU}_{n}$ and $C^{AU}_{p}$ are the Auger coefficient of electrons and holes in $m^6 s^{-1}$. This can be set in the electrical paramter editor.

Charge carrier transport

To describe charge carrier transport, the bi-polar drift-diffusion equations are solved in position space for electrons,

$$\boldsymbol{J_n} = q \mu_e n_{f} {\nabla E_{c}} + q D_n {\nabla n_{f}}$$

and holes,

$$\boldsymbol{J_p} = q \mu_h p_{f} {\nabla E_{v}} - q D_p {\nabla p_{f}}$$

Conservation of charge carriers is forced by solving the charge carrier continuity equations for both electrons,

$$\nabla \boldsymbol{J_n} = q (R-G+\frac{\partial n}{\partial t})$$

and holes

$$\nabla \boldsymbol{J_p} = - q (R-G+\frac{\partial p}{\partial t})$$

where $R$ and $G$ are the net recombination and generation rates per unit volume respectively.

Optical Generation Models

Three optical generation profiles are available:

Uniform – assumes constant photon flux throughout the active layer.
Exponential decay – Beer–Lambert absorption profile.
Transfer Matrix Method (TMM) – coherent wave optics with forward/backward propagation and reflection at interfaces.

These models can be linked directly into the drift–diffusion simulation to calculate position-dependent generation rates.

Dimensionality — Now Available in 3D

OghmaNano’s drift–diffusion engine now supports 1D, 2D, and full 3D device geometries with the same coupled physics (Poisson + electron/hole continuity, SRH trapping/recombination, optional ionic/excitonic terms). This lets you prototype quickly in 1D, validate lateral effects in 2D, and then study realistic architectures in 3D without changing tools.

Consistent physics: identical models across dimensions for apples-to-apples comparison.
Scalable meshing: orthogonal grids with per-axis sweeps (x/y/z) and boundary conditions applied on the full volume.
Opto-electrical coupling: uniform / Beer–Lambert / TMM optical generation profiles map directly onto the 3D mesh.

Advanced: Lua-Controlled Solver (Microcode)

For power users, the solver exposes a Lua microcode layer that controls the Newton iteration schedule and active physics at each micro-step. This enables ADI-style axis sweeps, block solves, and custom update schedules without recompiling the core.

What you can control

Iteration ordering & splitting: alternate x/y/z passes, block Gauss–Seidel/Jacobi, or fully coupled steps.
Active subsystems per pass: Poisson (solve_pos_*), e/h currents (solve_je_*/solve_jh_*), SRH traps, ions, singlets.
Sweep direction & stride: per-axis step_x, step_y, step_z (−1, 0, +1).
Convergence logic: early-exit thresholds and safety guards written directly in Lua.

Minimal example: 3D ADI sweep with SRH

Figure: JV sweep visualisation. Lua microcode lets you orchestrate axis sweeps and active physics at each pass.

a = dd_solver()
local count, cont = 0, true

while cont do
  -- Pass 1: Z-dominant
  a.set_newton_state("x")
  a.step_x, a.step_y, a.step_z =  1, -1, -1
  a.solve_pos_x, a.solve_pos_y, a.solve_pos_z = false, true,  true
  a.solve_je_x,  a.solve_je_y,  a.solve_je_z  = 0,     true,  true
  a.solve_jh_x,  a.solve_jh_y,  a.solve_jh_z  = 0,     true,  true
  a.solve_srh_e, a.solve_srh_h = true, true
  a.solve_nion,  a.solve_singlet = false, false
  local e1 = a:run()

  -- Pass 2: X-dominant
  a.set_newton_state("z")
  a.step_x, a.step_y, a.step_z = -1, -1,  1
  a.solve_pos_x, a.solve_pos_y, a.solve_pos_z = true,  true,  false
  a.solve_je_x,  a.solve_je_y,  a.solve_je_z  = true,  true,  false
  a.solve_jh_x,  a.solve_jh_y,  a.solve_jh_z  = true,  true,  false
  local e2 = a:run()

  local tot = e1 + e2
  print(("iter=%d residual=%.3e"):format(count, tot))

  cont = not (tot < 1e-7 or count > 10)
  count = count + 1
end

Flag reference (quick)

set_newton_state("x"|"y"|"z"|"all") — select block/state for the next micro-step.
step_x, step_y, step_z — sweep direction per axis: +1 forward, -1 reverse, 0 freeze.
solve_pos_* — include Poisson coupling along that axis in the Jacobian.
solve_je_*, solve_jh_* — include electron/hole current equations per axis.
solve_srh_e, solve_srh_h — update trap populations (electrons/holes).
solve_nion, solve_singlet — optional ionic/excitonic updates this pass.
:run() — executes one micro-iteration and returns a scalar residual.

This advanced control is ideal for tackling tough bias points, heavy trapping, or mobile-ion dynamics in full 3D meshes, and for prototyping new iteration strategies without recompilation.