SCLC 教程:快速入门 — 模拟空间电荷限制电流
空间电荷限制电流(SCLC)是这样一种输运区域:注入载流子占主导, 电流受其在薄膜中的运动限制,而非受产生过程限制。在理想的无陷阱器件中, 电流密度遵循 Mott–Gurney 定律: \( J = \frac{9}{8}\,\varepsilon\,\mu\,\frac{V^2}{L^3} \), 其中介电常数为 \( \varepsilon \),迁移率为 \( \mu \),电压为 \( V \),厚度为 \( L \)。 SCLC 测量(通常使用仅空穴或仅电子二极管)被广泛用于提取迁移率并评估 陷阱效应。在本快速入门中,你将配置一个 SCLC 结构,运行 JV 扫描,定位 J ∝ V² 区域,并观察陷阱或厚度如何移动曲线以及改变提取的迁移率。
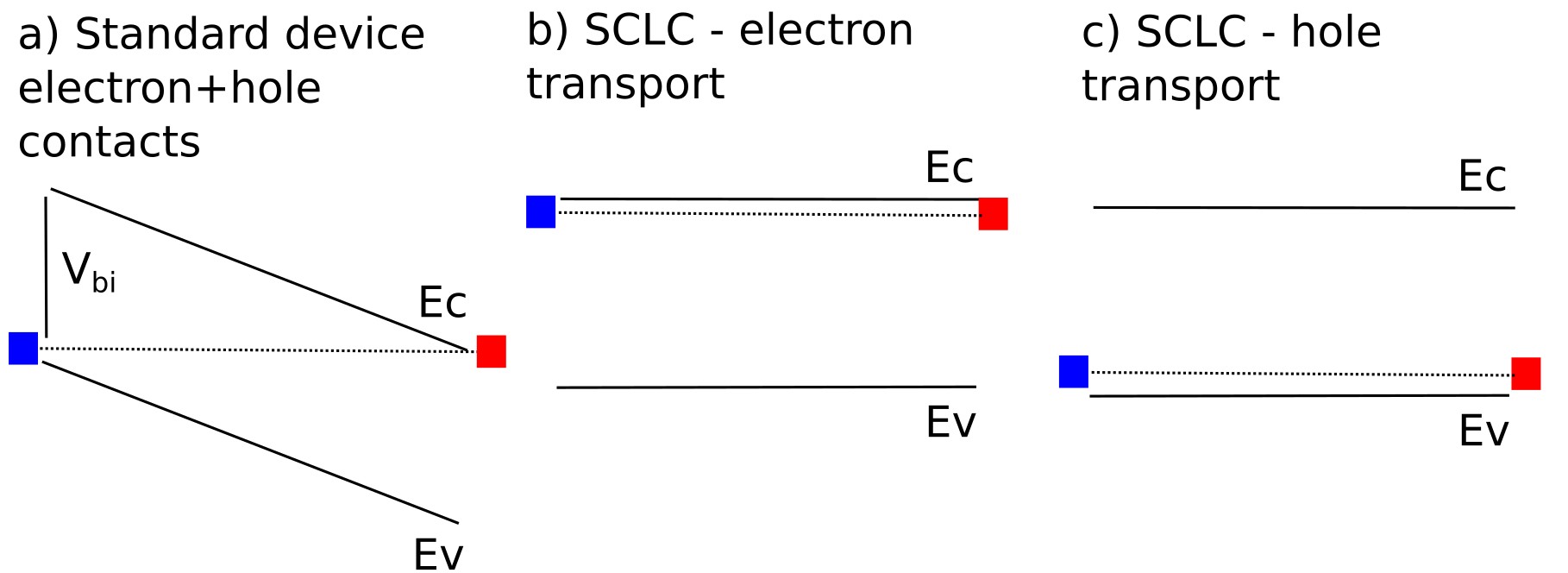
在 ?? 中,我们比较了用于控制哪些载流子能够进入器件的接触配置。在图 (a) 中,标准结构具有选择性电子与空穴接触,形成内建电势并允许电子与空穴的注入/抽取。通过调整接触能级或添加/选择输运/阻挡层,你可以实现单一载流子注入:在图 (b) 中,通过在两个接触处对导带提供低势垒并阻挡价带(空穴注入),形成仅电子器件(SCLC);在图 (c) 中,通过在两个接触处对价带对齐并阻挡导带(电子注入),形成仅空穴器件(SCL)。与 (a) 中的标准器件相比,(b,c) 的单载流子情形抑制复合并迫使电流受空间电荷限制输运控制,这非常适合提取载流子迁移率与接触效应。
步骤 1:创建一个新仿真
从 Windows 开始菜单启动 OghmaNano。主 OghmaNano 窗口将如 ?? 所示出现。
步骤 2:检查接触是否为 SCLC 设置
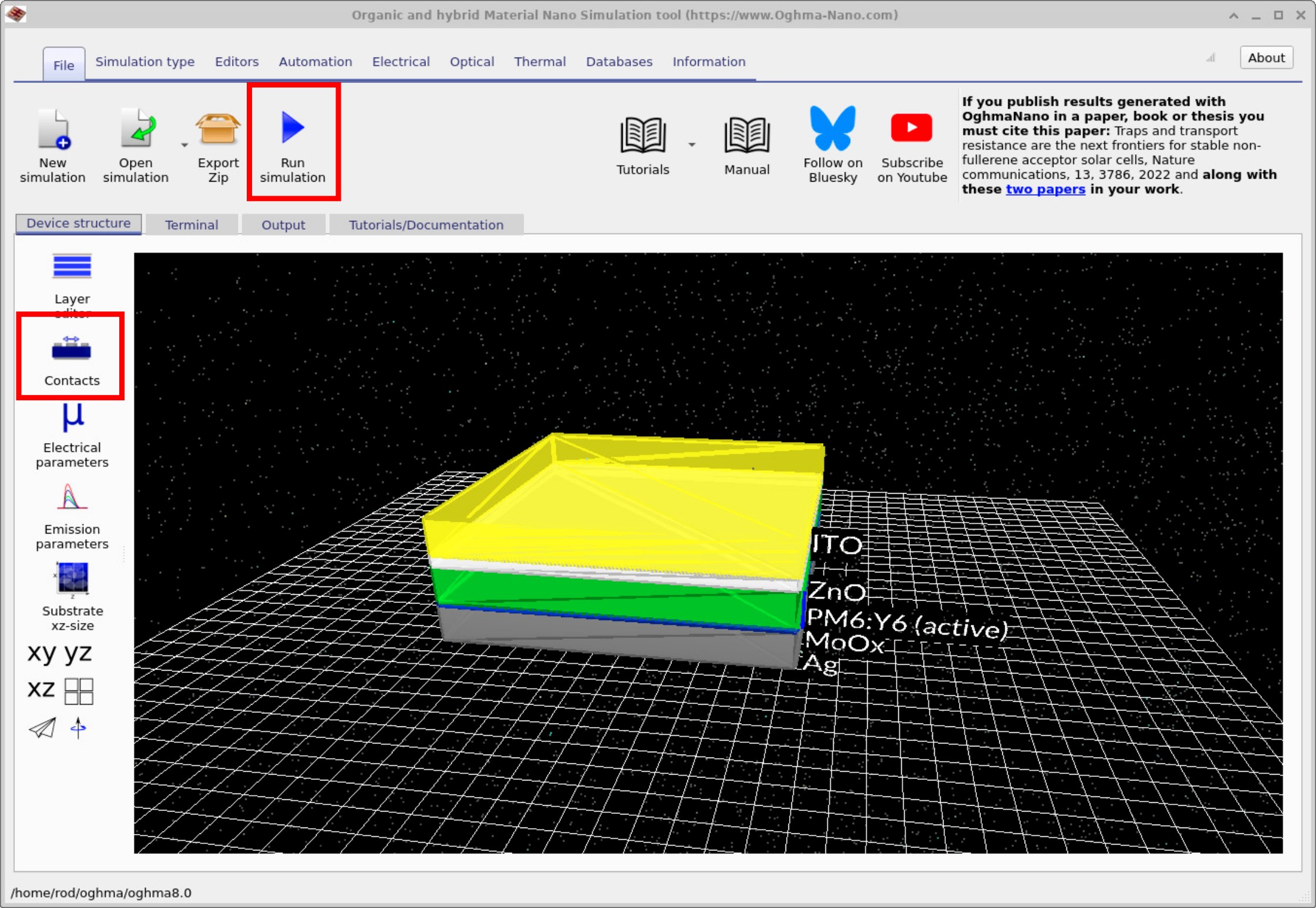
保存 SCLC 示例后,将出现主窗口 (??)。 该窗口显示器件的 3D 表示。 本窗口中我们将使用的两个关键按钮是 运行仿真按钮与 接触按钮。
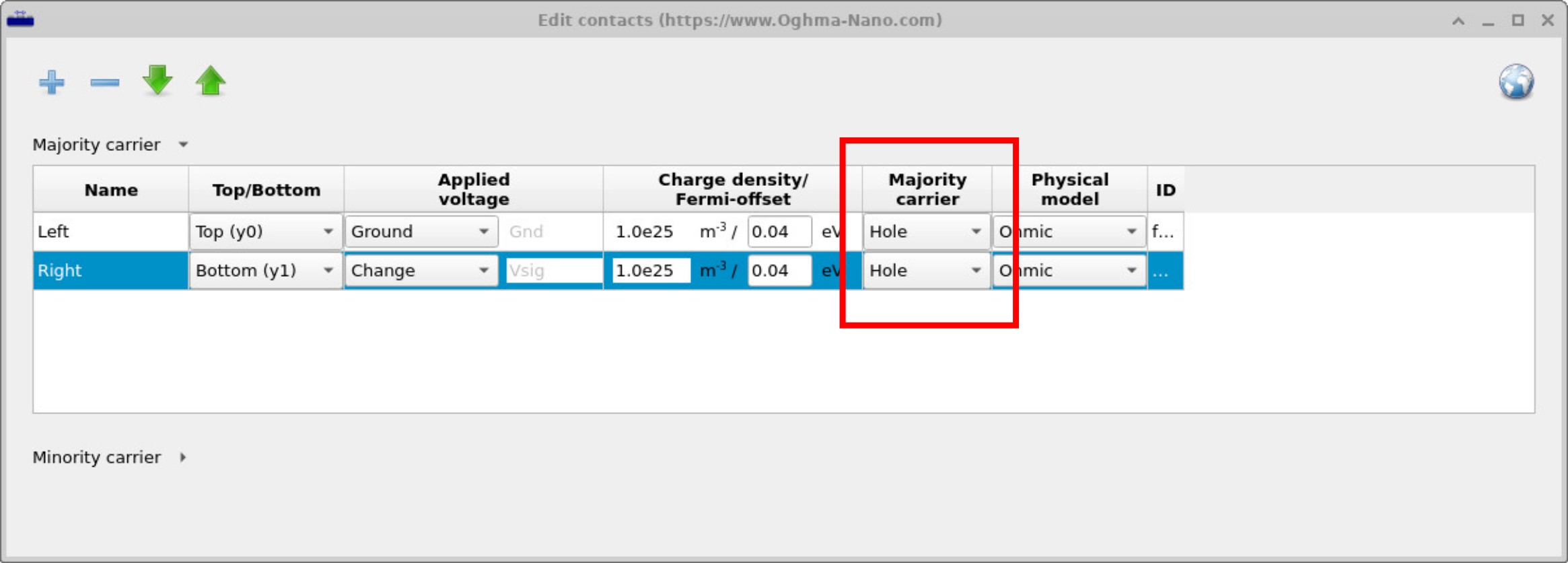
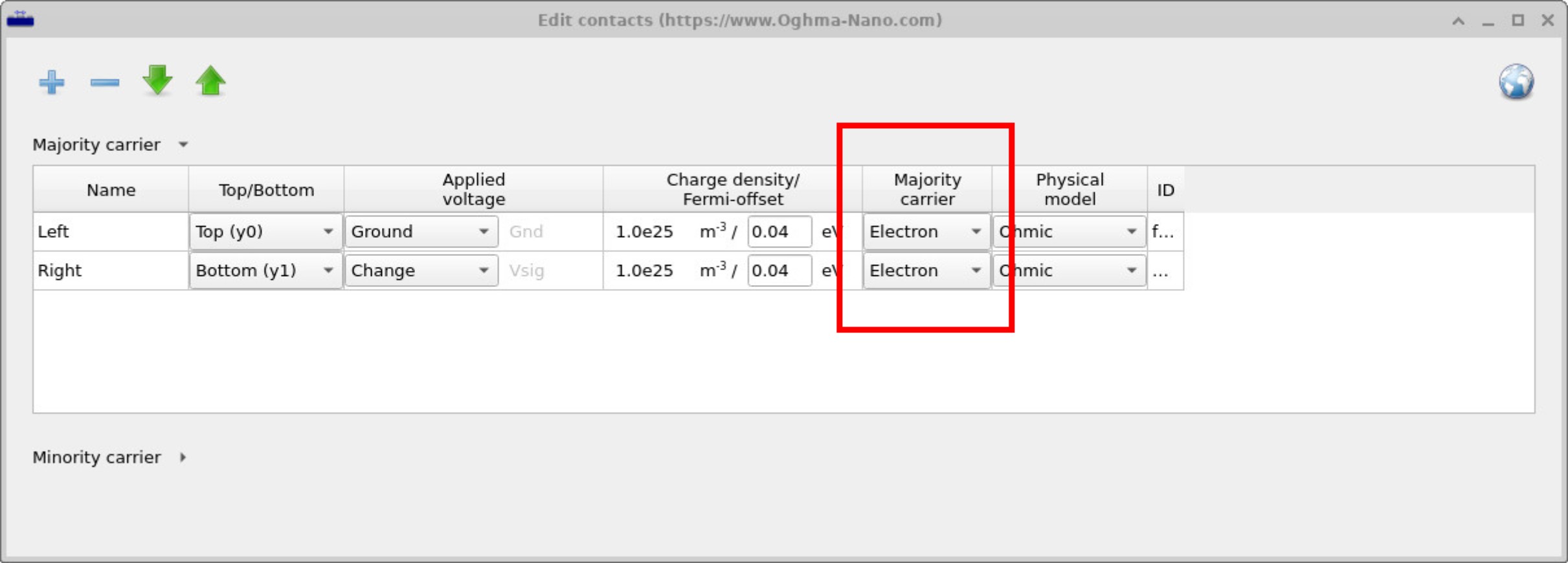
在点击 运行仿真 (或按 F9)运行仿真之前,我们需要先检查接触。 在主窗口 (??)中, 接触按钮在下方红色框中高亮。 点击它会打开接触编辑器。接触编辑器允许将两端接触设置为相同的载流子类型。 例如,它们都可以被定义为 空穴 接触 (??) 或都定义为 电子 接触 (??)。 换句话说,你选择一种载流子类型并将其应用到器件两侧。
这种设置与太阳能电池非常不同:太阳能电池的两个接触必须不同——一个电子接触和一个空穴接触。哪一侧是哪一类并不重要, 但这种不对称性对于分离电荷并驱动电流至关重要。而在 SCLC 测量中,这种对称性是刻意的。 如果两个接触都设置为 电子,器件测量 电子迁移率。 如果两个都设置为 空穴,则测量 空穴迁移率。 其逻辑很简单:接触注入其配置的载流子类型,而该载流子在器件中主导输运。
步骤 2:检查仿真是否在暗态运行
SCLC 几乎总是在暗态下进行。在运行实验之前,确保仿真也处于暗态条件。 这可以在 光学 功能区中将 光强(Suns) 设置为 0.0 来完成,如 ?? 所示。

步骤 3:开启更多可选输出
运行 SCLC 仿真前的最后一步是打开 JV 编辑器, 你可以从主窗口的 编辑器 → JV 编辑器 功能区访问它 (??)。 这将打开 JV 配置窗口 (??)。
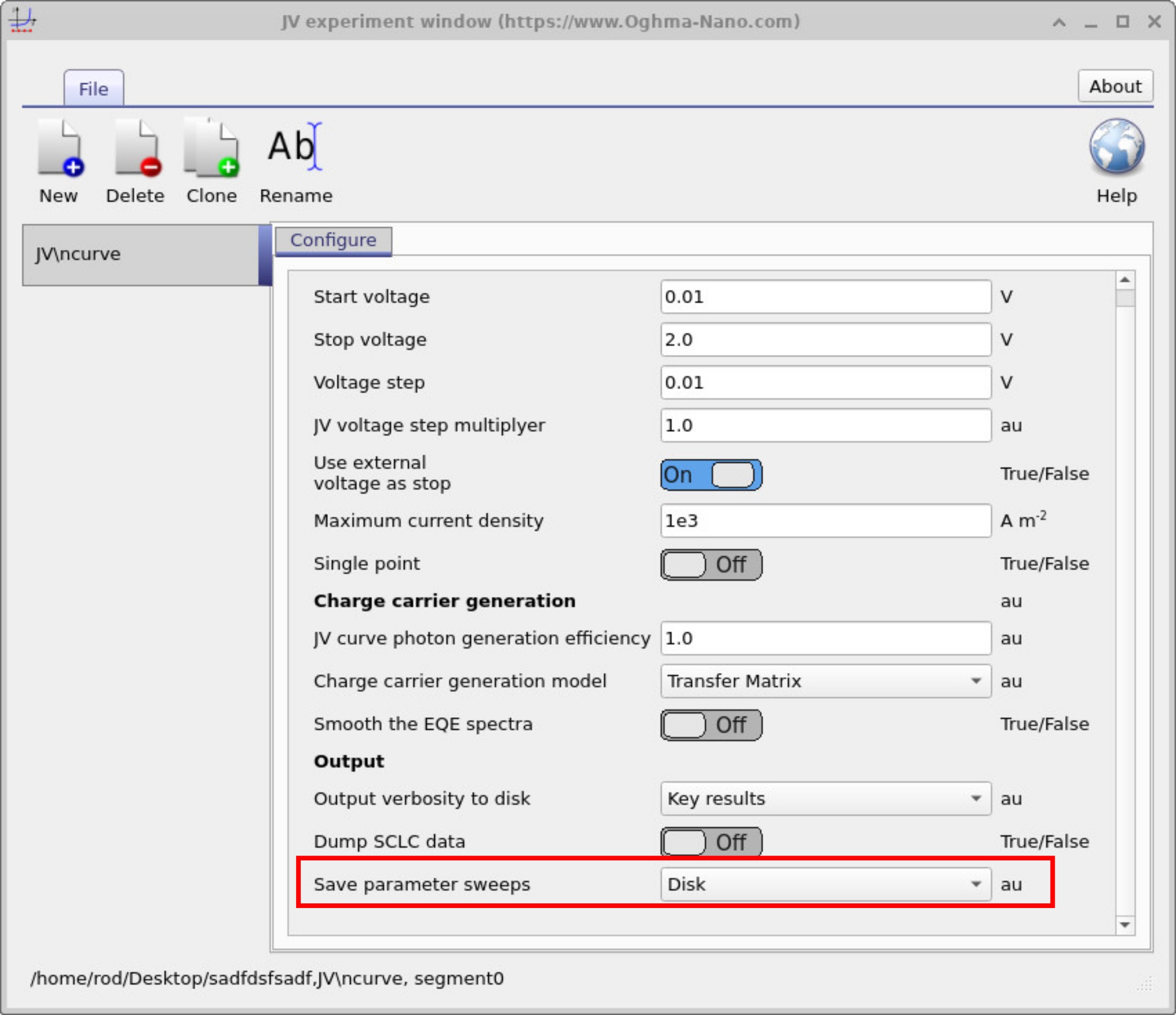
在该窗口中,确保 保存参数扫描 设置为 磁盘, 如 ?? 底部所示。 启用该选项可确保关键器件参数——如迁移率、载流子密度、 以及其他电学量——会随外加电压记录下来。 软件不会仅生成简单的 1D 快照,而是将这些数值在整个器件上进行积分 并存储,使其随后可随电压作图。 这对于 SCLC 分析至关重要,因为它使我们能够看到迁移率如何随电压演化 并确定从 SCLC 曲线中提取的数值。
默认情况下该功能通常是 关闭 的,因为将扫描数据写入磁盘 可能会降低仿真速度。在大多数情况下你希望最小化磁盘输出以保持运行高效。 但对于 SCLC,即使需要额外时间也值得启用,因为如果不启用 你将无法对器件中的迁移率趋势进行正确分析。
步骤 4:运行仿真
当 SCLC 仿真已完整准备好——将两个接触都设置为 空穴 或 电子,确认光已关闭, 并启用 保存参数扫描 选项——即可运行。 返回主窗口,通过点击 播放 按钮 或按 F9 启动仿真。
运行完成后,打开 输出 选项卡
(??)。
这里你将看到标准仿真输出,包括 jv.csv
以及 sweep 目录。双击 jv.csv 会打开 JV 图
(??),
显示典型的 SCLC 曲线。按下 L 再按 Shift+L
可将两轴切换为对数刻度,从而更容易识别
数据中的 SCLC 区域。
sweep 目录。
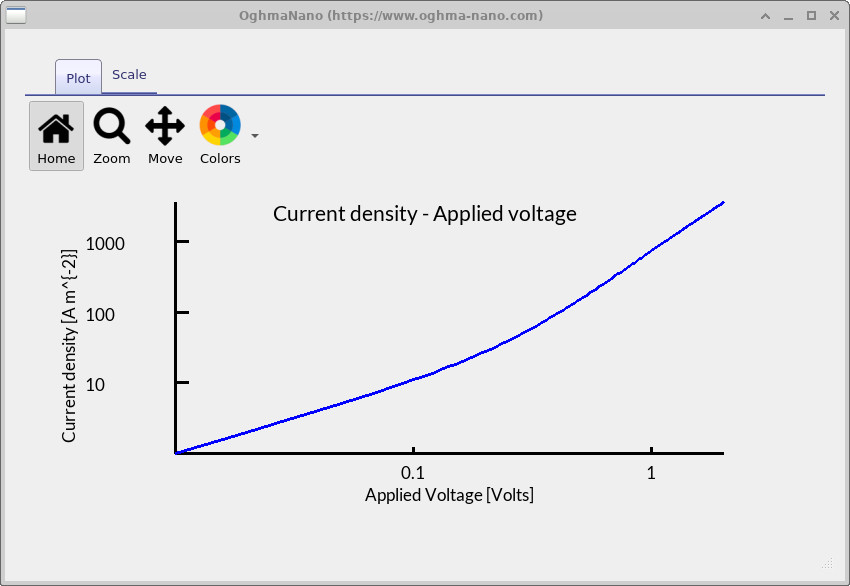
jv.csv 并按 L 然后 Shift+L 以在 log–log 坐标下绘图。JV 曲线揭示 SCLC 区域。
步骤 5:用“笨办法”提取 SCLC 迁移率
为了从 SCLC 测量中确定电荷载流子迁移率, 我们使用 Mott–Gurney 定律,它在无陷阱条件下将测得的电流密度 与外加电压联系起来。 关键步骤是在暗态测得的 JV 曲线中识别 SCLC 区域 (??)。 当接触对载流子的注入足够有效时就会进入 SCLC 区域, 此时电流不再由热产生载流子所限制, 而是由器件内空间电荷的累积所限制。 在该区域中电流密度随电压呈二次增长, 满足 \( J \propto V^2 \)。
在电流密度—电压的 log–log 图上,SCLC 区域可通过 斜率约为 2.0 的直线段来识别。 在更低电压下斜率更接近 1.0,反映由平衡载流子主导的欧姆导电。 在更高电压下,如果陷阱填充、串联电阻或高场效应变得重要, 电流可能会再次偏离二次行为。 因此迁移率应当只在斜率接近 2 的中间电压区间提取, 因为这对应于 Mott–Gurney 定律所假设的无陷阱 SCLC 条件。
对于无陷阱的空间电荷限制电流,电流密度为
$$ J = \frac{9}{8}\,\varepsilon \mu \frac{V^2}{L^3}. $$
整理得到迁移率:
$$ \mu = \frac{8}{9} \cdot \frac{J L^3}{\varepsilon V^2}. $$
代入代表性数值:
- \( L = 100~\text{nm} = 1.0\times10^{-7}~\text{m} \;\;\Rightarrow\;\; L^3 = 1.0\times10^{-21}~\text{m}^3 \)
- \( \varepsilon_r = 3.0 \),\( \varepsilon_0 = 8.85\times10^{-12}~\text{F·m}^{-1} \),因此 \( \varepsilon = 2.655\times10^{-11}~\text{F·m}^{-1} \)
- \( V = 1.0~\text{V} \)
- \( J \approx 1.0\times10^{3}~\text{A·m}^{-2} \)
则:
$$ \mu = \frac{8}{9} \cdot \frac{ (1.0\times10^{3})(1.0\times10^{-21}) } { (2.655\times10^{-11})(1.0^2) } = 3.35\times10^{-8}~\text{m}^2\text{V}^{-1}\text{s}^{-1}. $$
以 cgs 单位表示,这对应于
该算例展示了如何使用 Mott–Gurney 关系式 从 SCLC 区域的 JV 曲线直接提取迁移率。
步骤 6:绘制器件内部的实际迁移率
仿真的一个真正优势是你并不受限于
解析模型的预测。相反,你可以直接查看
模拟器件内部并检查物理量如何随电压
施加而演化。在这里,我们可以探索存储在 sweep 文件夹中的结果,
其在
?? 中显示。
打开该文件夹会出现文件列表
(??),
这些文件包含随电压保存的器件参数。这些参数包括
产生率、载流子密度、复合率以及许多其他量。
对于迁移率分析,关键文件是 mun.csv 与 mup.csv,
它们分别报告模拟的电子与空穴迁移率。你选择哪个文件取决于
之前将器件配置为电子接触还是空穴接触。
在本示例中,我们关注电子输运,因此检查
mun.csv 输出,如
?? 所示。
该图揭示迁移率如何随外加电压变化。
上升趋势出现在包含陷阱的器件中。随着偏压增大, 更多陷阱被填充并有更多载流子释放到自由态, 从而导致表观迁移率上升。这种行为超出了简单的 Mott–Gurney 描述,并凸显了仿真的价值:它不仅 再现电流–电压曲线,还让我们看到塑造器件性能的 底层物理过程。
sweep 目录的内容,可从
输出 选项卡访问。这里存储了许多器件参数,
可以随电压作图。
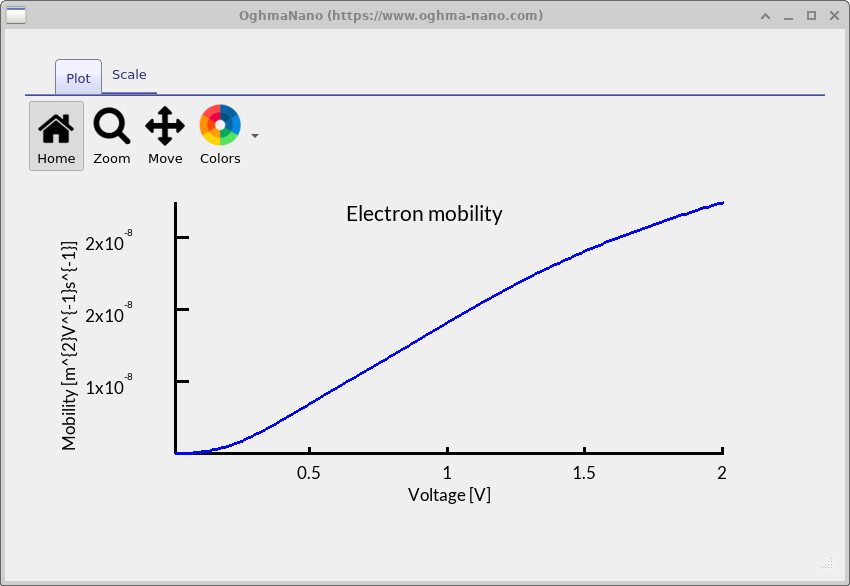
sweep 目录中打开 电子迁移率 结果,以查看迁移率随电压的变化。
将 第 5 节 的解析结果与 第 6 节 的数值结果进行比较,我们得到 解析迁移率约为 \(3.35\times10^{-8}\ \mathrm{m^2\,V^{-1}\,s^{-1}}\),而 SCLC 情形下的仿真值约为 \(2\times10^{-8}\ \mathrm{m^2\,V^{-1}\,s^{-1}}\)。这里差异相对较小,但它凸显了一个常见结果:在对比解析与数值方法时, 简化的解析模型(例如理想、无陷阱的 Mott–Gurney 假设、完全欧姆注入、均匀电场、无 串联电阻或场依赖性)可能会与解析陷阱、空间变化以及 非理想接触的完整器件仿真存在差别。因此,即使在 SCLC 中,解析值与数值值也不必完全一致——但其趋势应当 一致。
👉 下一步: 现在继续到 钙钛矿器件仿真