Quick start: Optical filter overview

In this quick start we use OghmaNano’s optical filter solver to calculate how light is reflected and transmitted by multilayer thin-film stacks at normal incidence. Such stacks can be designed as antireflection coatings, mirrors, or band-pass filters.

1. Background:

Light travelling through a thin film can be thought of as a forward and a backward wave. As the wave passes through a layer of thickness \(d\) and refractive index \(n\), it acquires a phase shift \(\delta = \tfrac{2\pi}{\lambda}\,n d\), where \(\lambda\) is the wavelength in free space. The behaviour of the wave in the layer can be written using a 2×2 transfer matrix \[ M = \begin{bmatrix} \cos(\delta) & \tfrac{i}{n}\sin(\delta) \\ i n \sin(\delta) & \cos(\delta) \end{bmatrix}, \] which relates the electric field amplitudes entering and leaving the layer.

For a stack of layers, the overall response is found simply by multiplying the matrices of all layers: \[ M_\text{total} = \prod_{j=1}^{N} M_j. \] Once the total matrix is known, the reflection and transmission of the stack can be calculated. If the incident medium has refractive index \(n_0\) and the substrate has refractive index \(n_s\), the reflection and transmission coefficients are extracted from \(M_\text{total}\), and the measurable reflectance and transmittance are given by \[ R = |r|^2, \qquad T = \frac{n_s}{n_0}\,|t|^2. \]

By adjusting the thicknesses and refractive indices of the layers, one can design filters with tailored optical properties. A single quarter-wave layer can suppress reflection at its design wavelength, while alternating high- and low-index quarter-wave layers produce a Bragg reflector with a strong stop band.

2. Getting started:

To start your first optical filter calculation, open the New simulation window from the File ribbon in the main menu. Double-click the Optical filter example (see ??) and save the simulation to a folder on your disk. You will then see the main window (see ??) with a multilayer stack of around ten alternating layers. Click the Run simulation (play) button to compute the spectra; once finished, the results appear in the Output tab (see ??).

Examining the Output

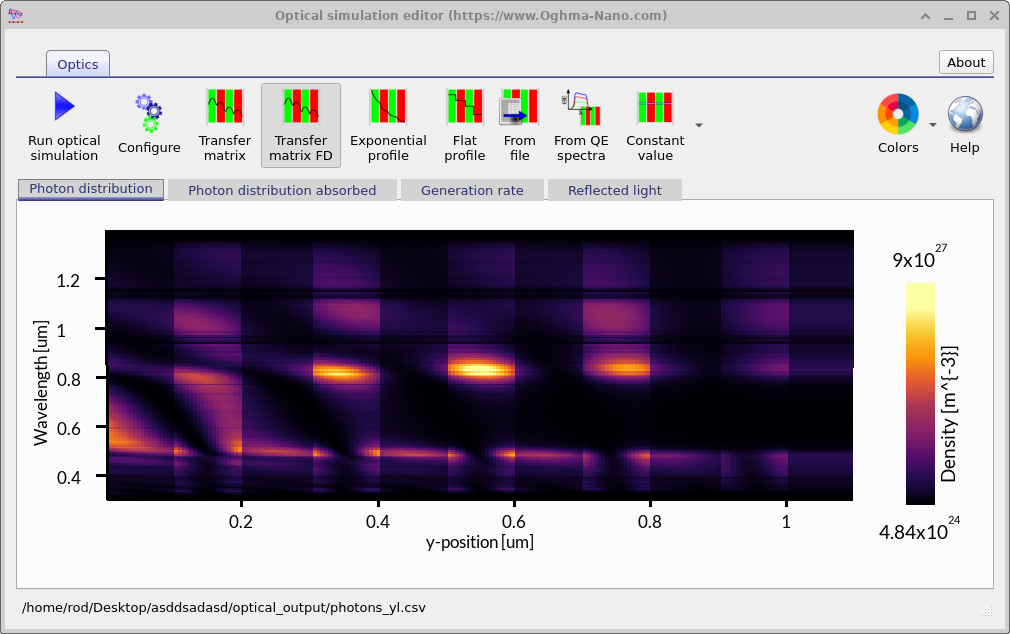
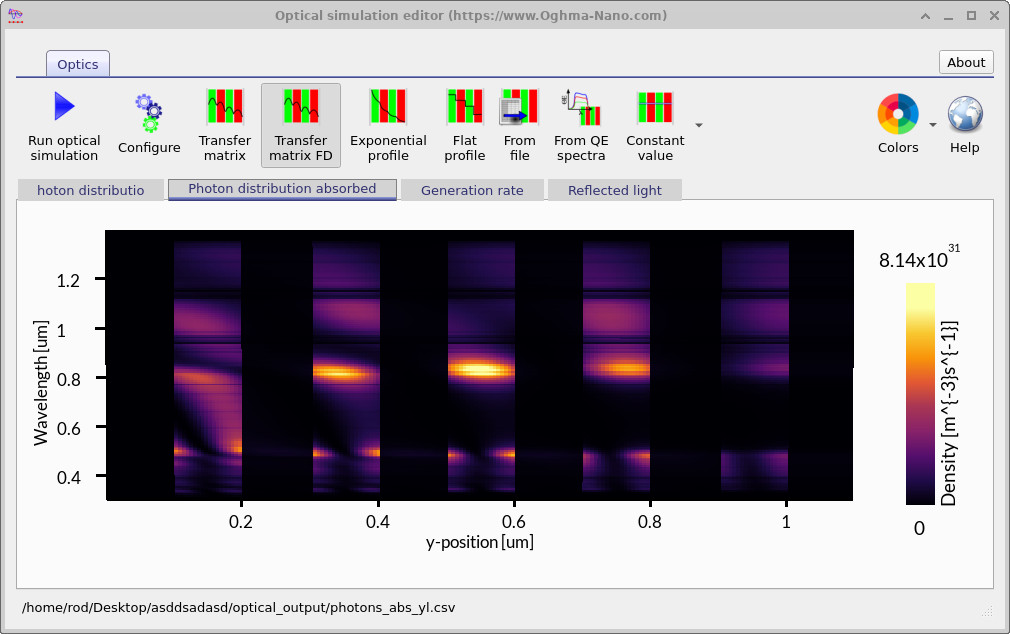
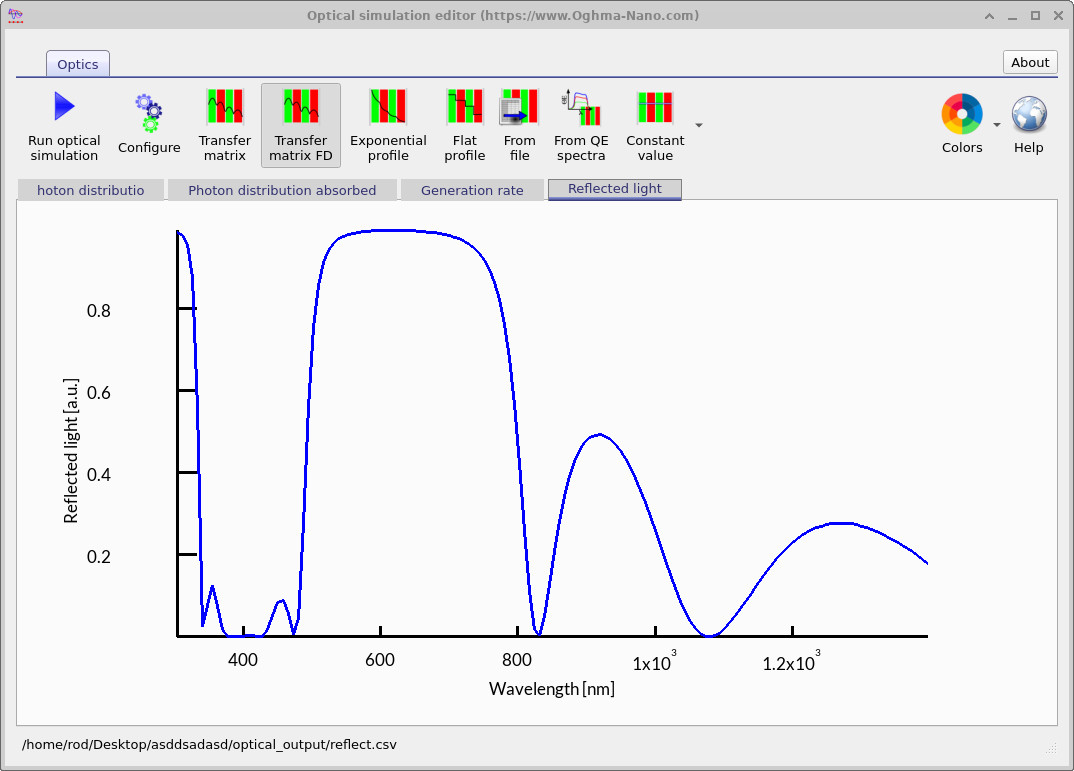
After running the simulation, double-click on Optical Output from ??. This will open the Optical Simulation Editor. The editor contains several tabs. The first tab, Photon distribution, is shown automatically (see ??). Here the photon density within the cavity is displayed, and the layered structure of the filter is clearly visible as vertical stripes. The second tab, Photon distribution absorbed (see ??), shows where photons are absorbed. In this example, absorption is weak but nonzero, because one of the materials has been set with a small absorption coefficient \(\alpha\). Finally, the Reflected light tab (see ??) displays the reflectance spectrum. The result demonstrates strong reflection between about 500 nm and 800 nm, while light outside this band is transmitted to varying degrees, characteristic of a Bragg-type filter.

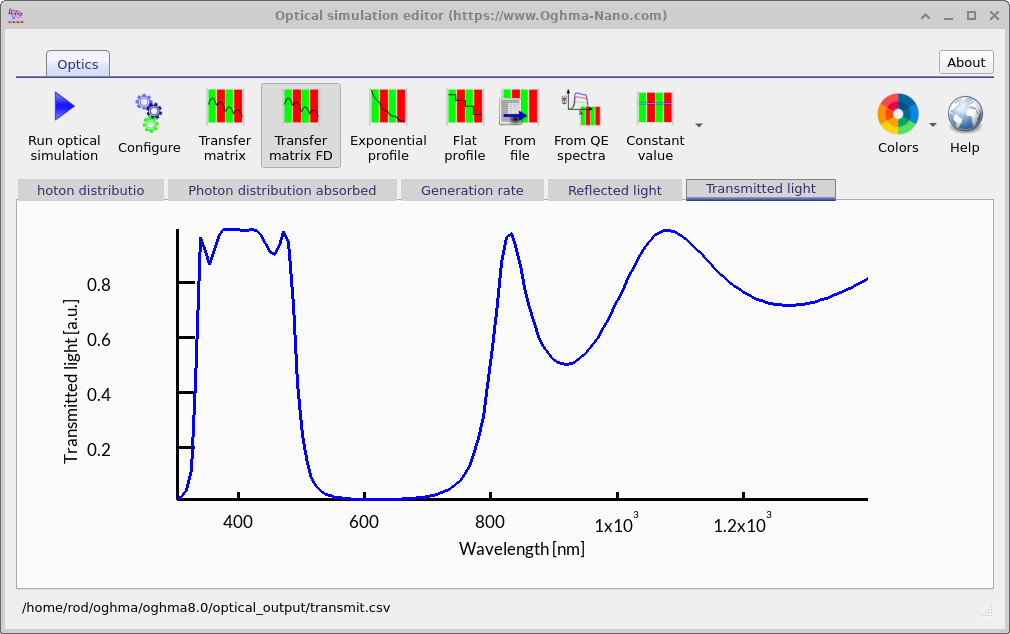
The Transmitted light spectrum confirms the band-stop behaviour of the filter. Light between about 300 nm and 500 nm is transmitted effectively, while wavelengths in the 500–800 nm range are strongly blocked. At longer wavelengths above 800 nm, some transmission reappears, showing the multi-band nature of the filter response.

Editing the filter

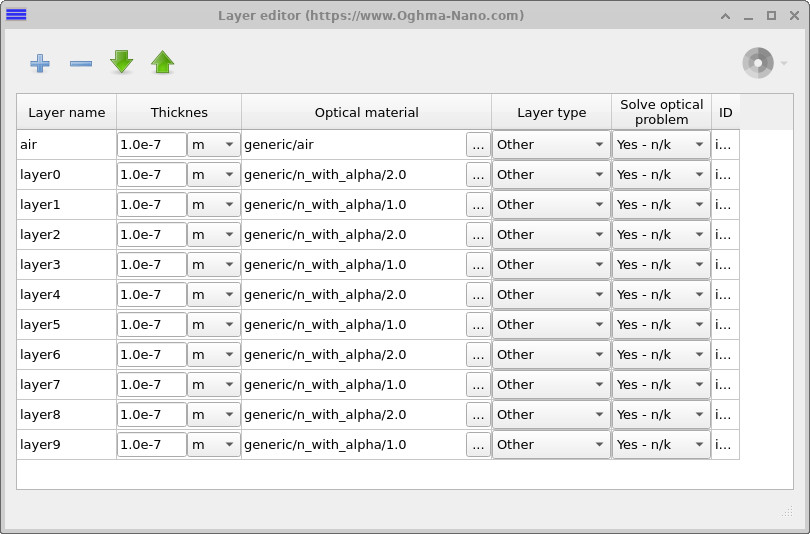
To inspect or modify the stack, open the Device structure tab in the main window and click Layer editor (see ??). The editor lists each layer in the device with its thickness, optical material, and settings. You can edit layer thicknesses directly in the table, change materials, add or remove layers, and reorder them as needed for your filter design.