Shockley–Read–Hall (SRH) Recombination Model
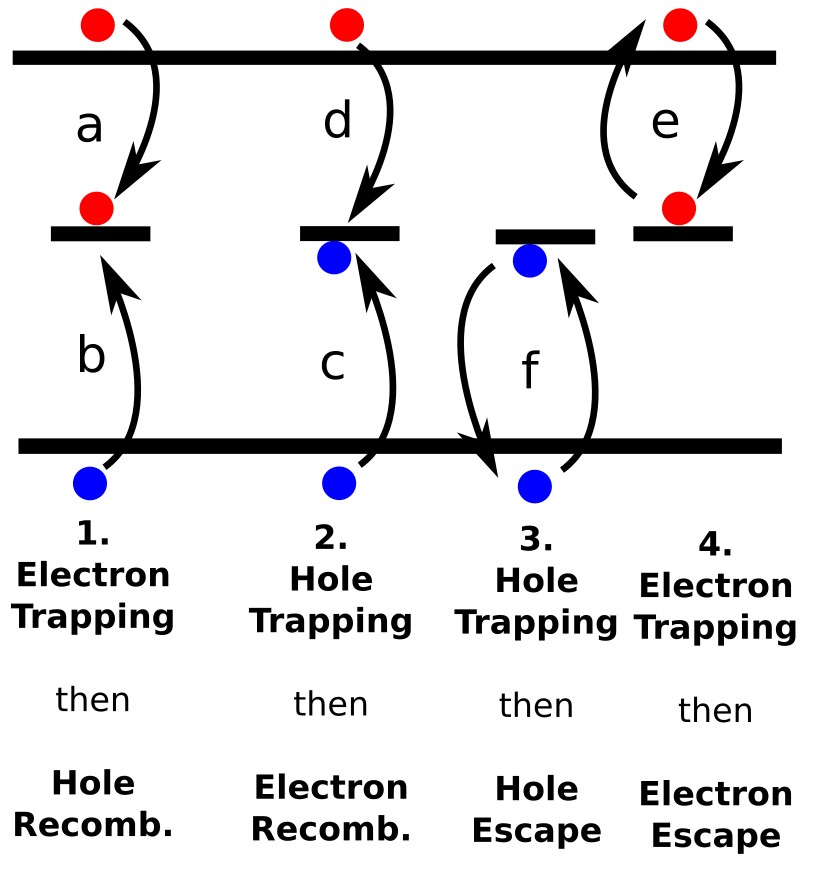
(2) Hole trapping (d) followed by electron recombination (c).
(3) Hole trapping (f) with subsequent thermal hole escape.
(4) Electron trapping (e) with subsequent thermal electron escape.
Shockley–Read–Hall (SRH) recombination describes carrier loss through localized defect states (traps) within the band gap. It is a trap-assisted process: an electron (or hole) is first captured into a defect state, and then may either recombine with an opposite carrier or re-emerge by thermal excitation. ?? illustrates the four main pathways for a single mid-gap trap state, with transitions labelled (a–f):
- 1. Electron trapping: capture of an electron (a), followed by recombination with a trapped hole (b).
- 2. Hole trapping: capture of a hole (d), followed by recombination with a trapped electron (c).
- 3. Hole trapping with escape: capture of a hole, followed by thermal re-emission (f).
- 4. Electron trapping with escape: capture of an electron, followed by thermal re-emission (e).
These processes show that the same trap can mediate both recombination and carrier release. SRH recombination is inherently a two-stage mechanism: first, a carrier is captured (a, d), and only later does recombination occur when the opposite carrier is captured (b, c). If no opposite carrier arrives, the trapped carrier may thermally escape (e, f). The overall efficiency of SRH recombination depends on trap density, energy level within the band gap, carrier capture cross-sections, and the relative lifetimes of trapped carriers.
Standard SRH Recombination Rate
The net trap-assisted recombination rate under the SRH model is:
\[R_{\mathrm{SRH}} = \frac{np - n_{i}^{2}} {\tau_{p}(n + n_{1}) + \tau_{n}(p + p_{1})} \]
where:
- \(\tau_{n}\), \(\tau_{p}\) are the electron and hole lifetimes associated with the trap,
- \(n_{1} = N_{C} \exp\!\big(-(E_{C} - E_{t})/k_{B}T\big)\) is the effective electron density when the trap lies in equilibrium,
- \(p_{1} = N_{V} \exp\!\big(-(E_{t} - E_{V})/k_{B}T\big)\) is the corresponding hole density,
- \(E_{t}\) is the trap energy level, and \(n_{i}\) is the intrinsic carrier concentration.
In this formulation, the recombination process is described in terms of a single trap level. The SRH model is therefore widely used because it provides an analytical expression that is straightforward to evaluate and captures the essential role of defect states in recombination.
Limitations of the Standard SRH Model
While powerful, the standard SRH equation comes with several important limitations:
- Single-level approximation — it accounts for only one discrete trap energy, whereas real semiconductors (particularly organics and disordered systems) typically contain a broad distribution of trap states.
- No explicit electrostatics — the model treats traps as purely recombination centers. Charges temporarily captured in traps are not included in the electrostatic potential of the device, so their effect on space charge and internal fields is ignored.
- Purely recombination-focused — the expression does not describe trapping and de-trapping dynamics explicitly, only their net effect as recombination.
To overcome these limitations, one must explicitly solve the SRH formalism across a distribution of trap states, allowing both the recombination rate and the trap occupation (and thus their electrostatic contribution) to be correctly represented. This more general treatment is described here.
In OghmaNano, the standard SRH recombination term can be enabled or disabled in the Electrical parameter editor, and the lifetimes \(\tau_{n}\) and \(\tau_{p}\) can be specified by the user.
Using SRH in OghmaNano
Where to go next
- Explore Shockley–Read–Hall (SRH) recombination in more detail, including how the model is derived and its analytical formulation.
- Visit the Electrical Parameter Editor to see how trap states and SRH lifetimes are configured in OghmaNano.
🎯 By following these sections, you’ll move from the analytical SRH model to its dynamic simulation and practical parameterization, bridging theory and device modeling.