Electrical Parameter editor

1. Introduction

In OghmaNano, the Electrical parameter editor provides the interface for defining the transport and recombination properties of electrically active layers. To access it, click the Electrical parameters button in the Device structure tab of the main simulation window (see ??). When opened, the Electrical parameter editor displays a set of input fields where you can specify key quantities such as carrier mobilities, densities of states, recombination constants, and fundamental material properties like bandgap and permittivity (see ??). Importantly, only layers that have been marked as active in the Layer editor will appear in the Electrical parameter editor. If a layer is not set as active, its electrical properties cannot be edited, since drift–diffusion and recombination processes are not solved in those regions.

2. Basic electrostatics and drift–diffusion equations

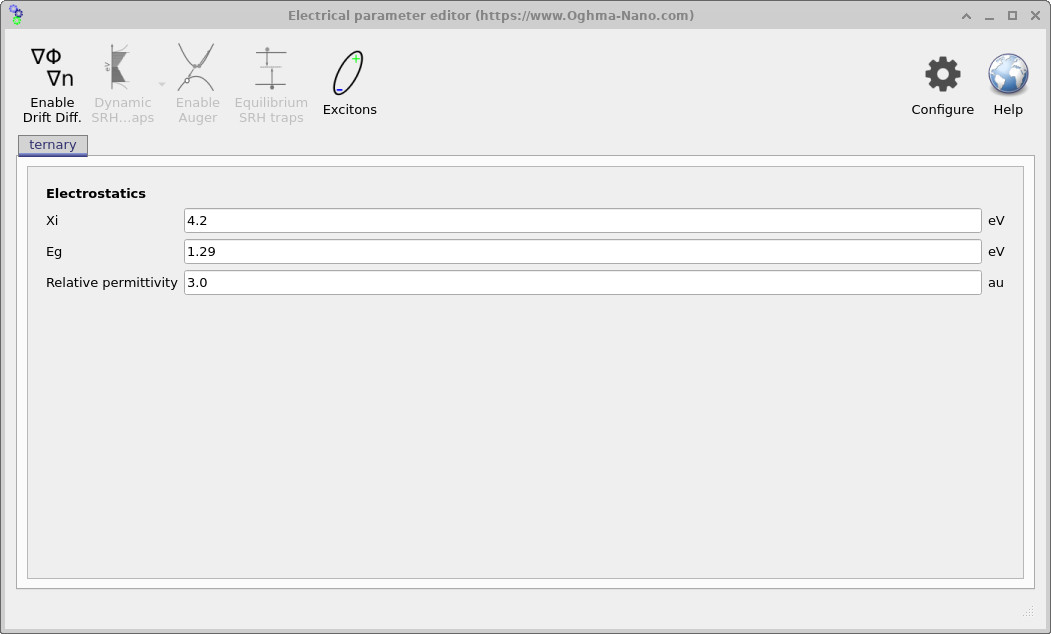
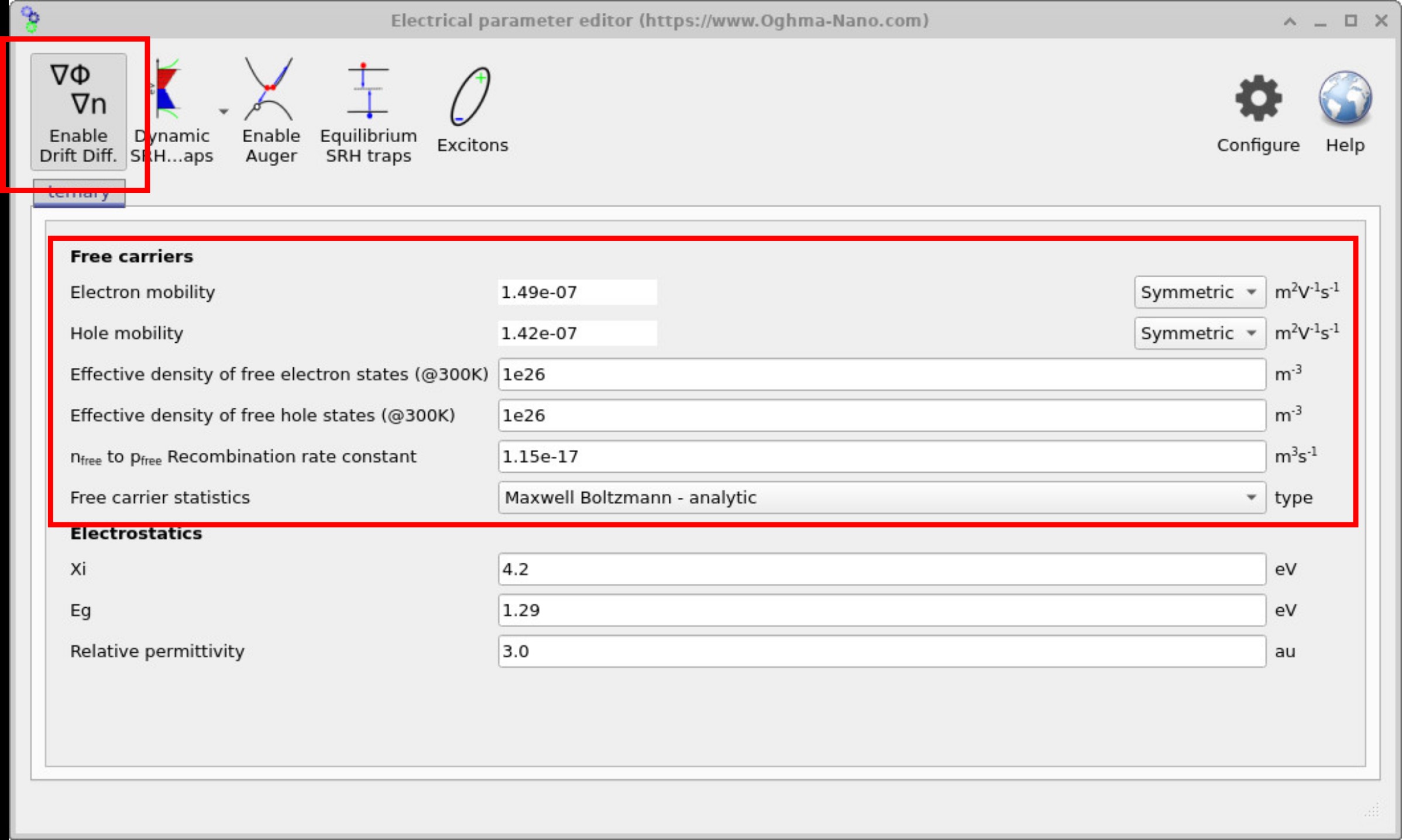
Figure ?? shows the Electrical parameter editor with no additional solver buttons activated. In this state, the drift–diffusion equations are disabled, but the Poisson equation is still solved. The interface therefore displays only the parameters needed for electrostatics: the electron affinity (χ), the band gap (E_g), and the relative permittivity (ε_r). These quantities define how the potential is distributed across the device.

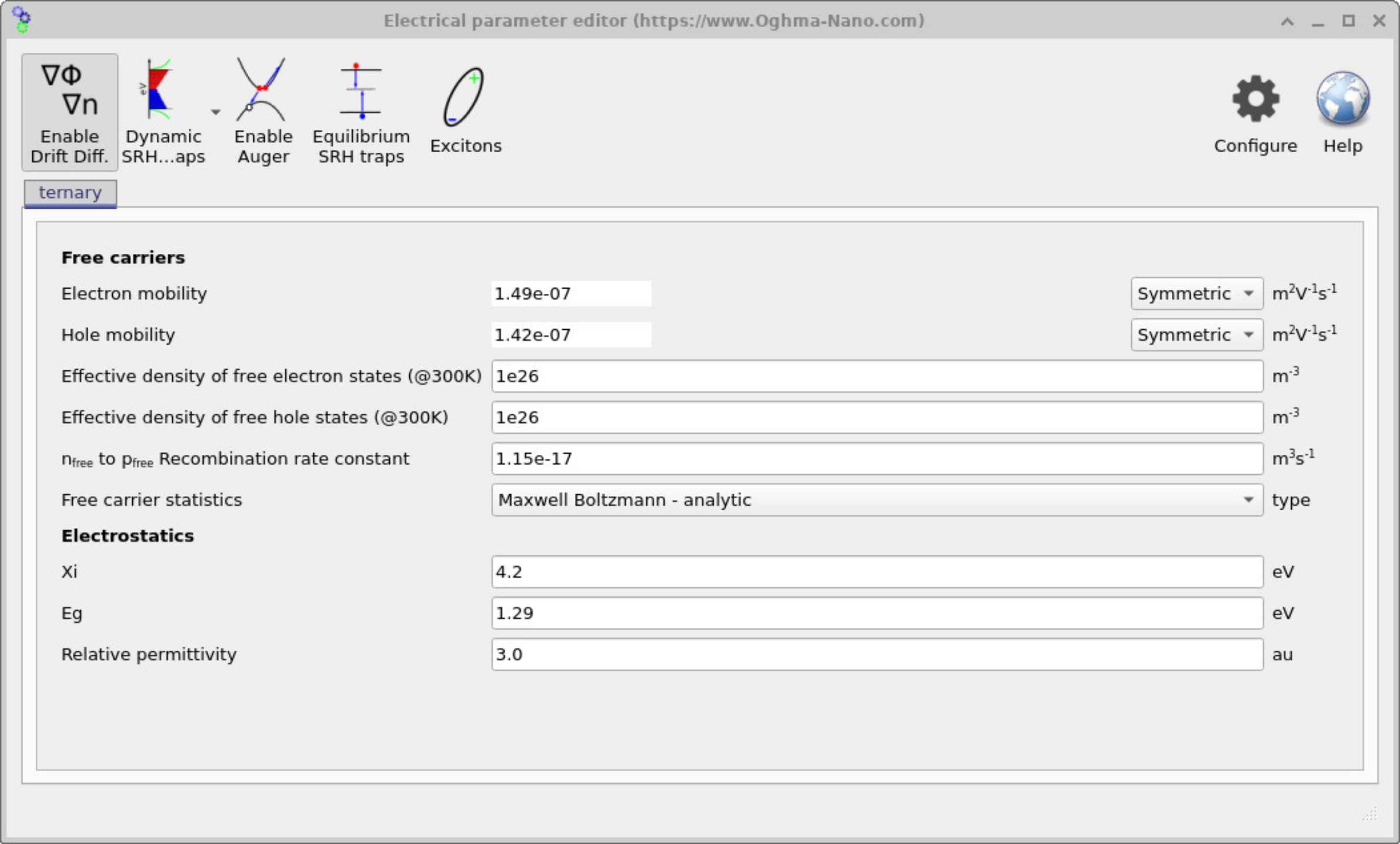
In contrast, Figure ?? shows the same editor with the Enable Drift Diffusion button depressed. When activated, the drift–diffusion solver is enabled and a wider set of parameters becomes available. These include the electron mobility, hole mobility, effective densities of states, and the free-to-free recombination rate constant. Users can also select the form of the free carrier statistics, e.g. Maxwell–Boltzmann or Fermi–Dirac, depending on the material system.

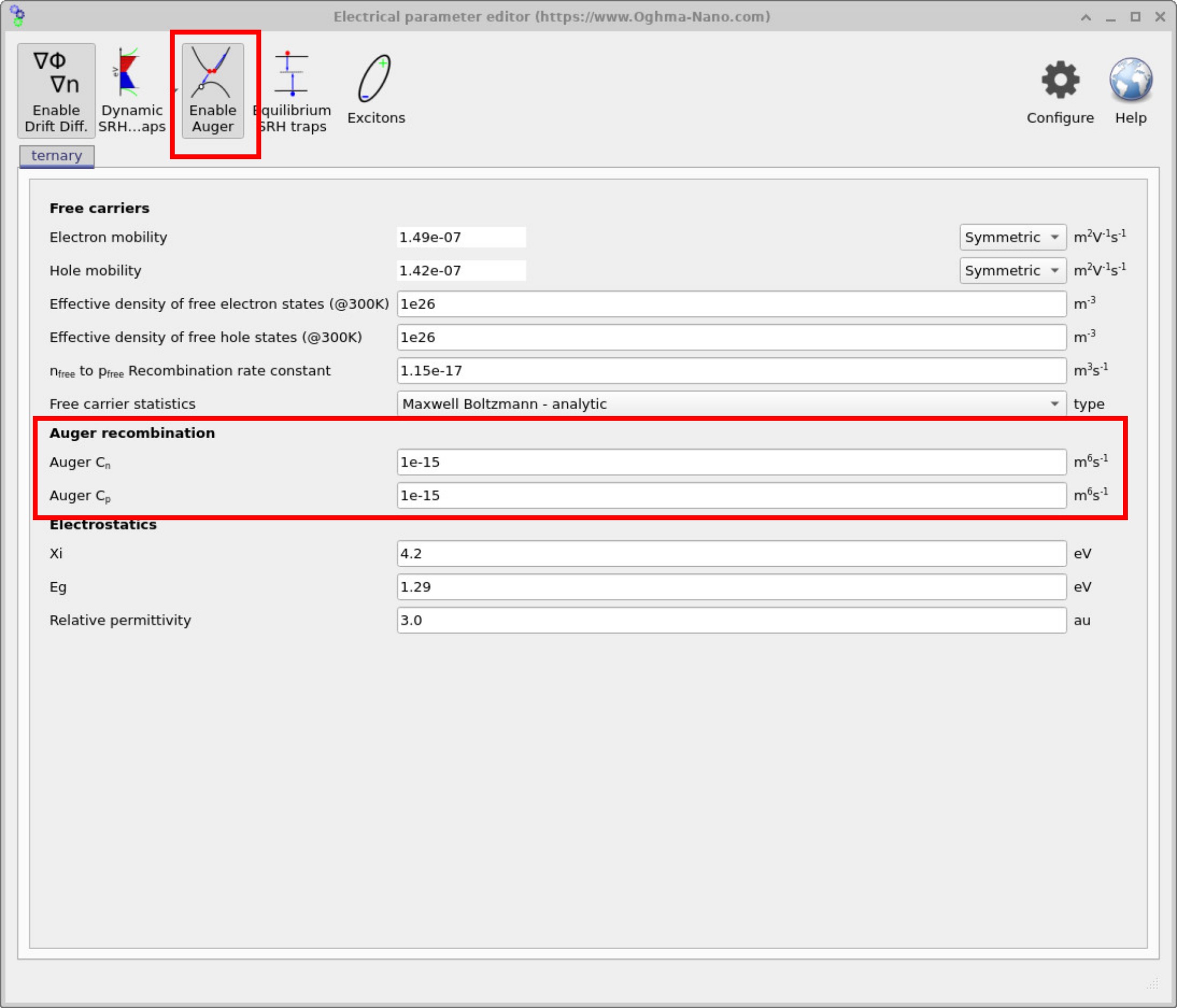
3. Auger recombination and equilibrium SRH traps

Figure ?? shows the Electrical parameter editor with the Enable Auger button depressed. When active, the interface displays additional fields for the Auger recombination constants (\(C_n\) and \(C_p\)). These parameters describe three-particle recombination processes, which become particularly significant at high carrier densities.

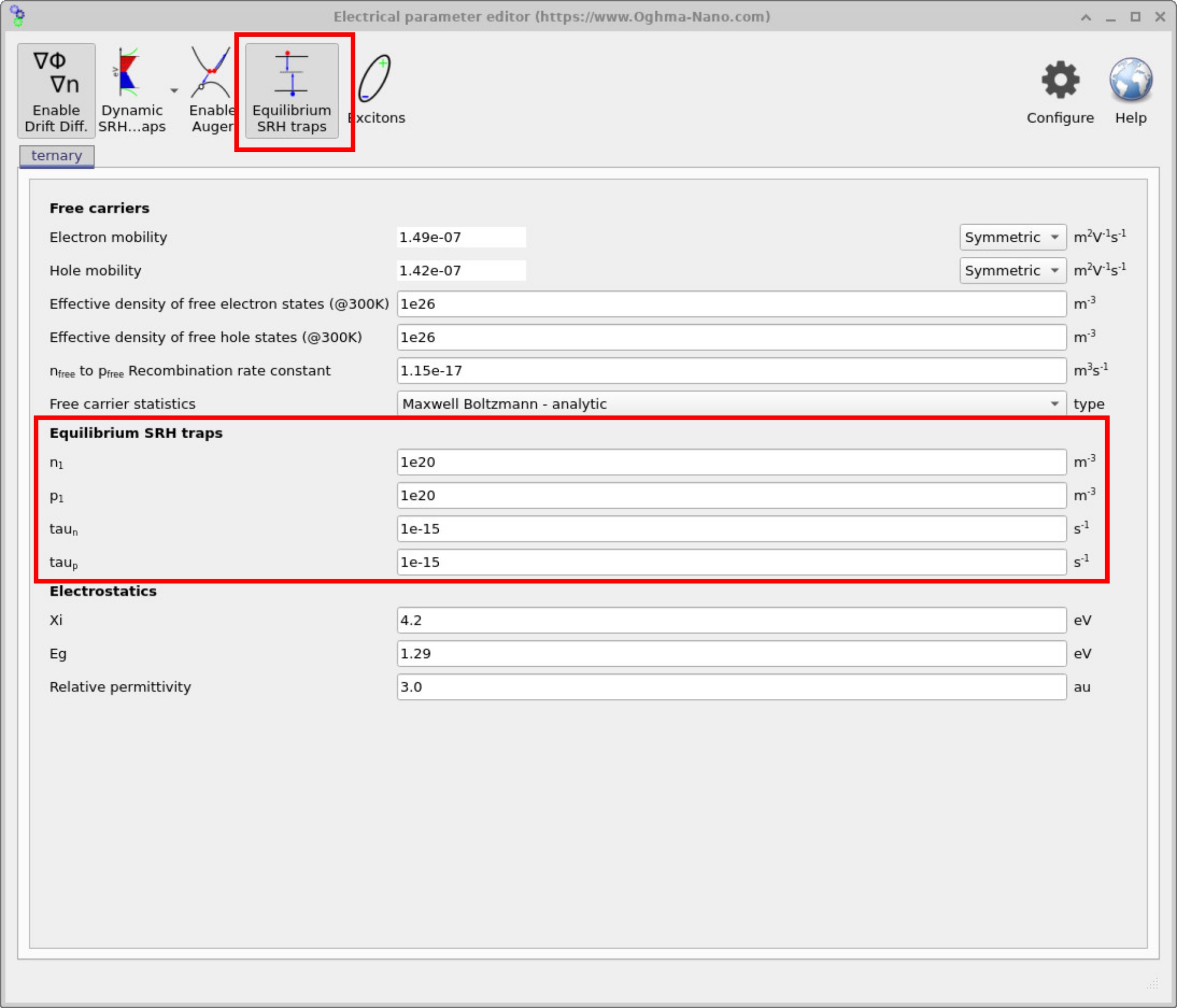
Figure ?? shows the editor with the Equilibrium SRH traps option enabled. This activates input fields for specifying trap parameters, including the electron and hole trap densities (\(n_1\), \(p_1\)) and their associated lifetimes (\(\tau_n\), \(\tau_p\)). These values are used in the standard steady-state Shockley–Read–Hall (SRH) recombination model:

\[ R_{\mathrm{SRH}} = \frac{np - n_i^2}{\tau_p (n + n_1) + \tau_n (p + p_1)} \]

This implementation corresponds to the classical equilibrium SRH model. It does not include the more advanced non-equilibrium SRH dynamics (trapping and escape), which are handled separately under the dynamic SRH traps option.

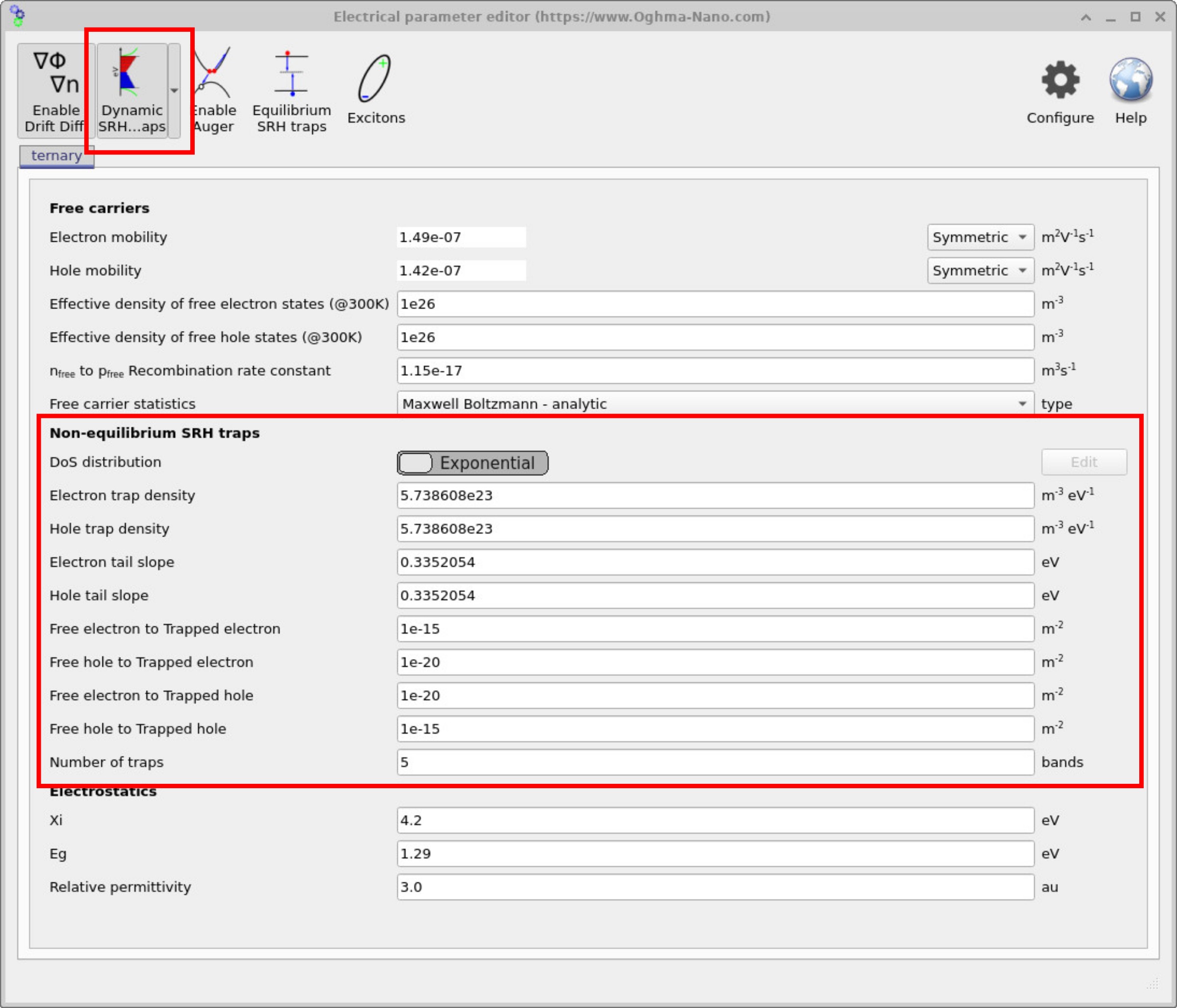
4. Dynamic Shockley–Read–Hall trapping and recombination

By enabling the Dynamic SRH traps option together with the drift–diffusion solver, OghmaNano solves a full set of Shockley–Read–Hall trapping and escape equations at every mesh point. This allows the simulation to capture the transient dynamics of charge carriers interacting with traps.

Figure ?? shows the default configuration, in which two exponential tails of trap states are solved beneath each mesh point. Parameters include:

• Electron and hole trap densities
• Electron and hole tail slopes (Urbach energies)
• Capture cross-sections:
  • Free electron → trapped electron (trapping)
  • Free hole → trapped hole (trapping)
  • Free electron → trapped hole (recombination)
  • Free hole → trapped electron (recombination)
• Number of traps — the number of discrete trap energy levels used to approximate the continuous distribution (this is not the trap density itself).

Solving these equations is particularly important when modelling highly disordered semiconductors, since it captures not only recombination via the exponential tail of trap states, but also the additional charge stored in those traps, which can strongly affect device performance.

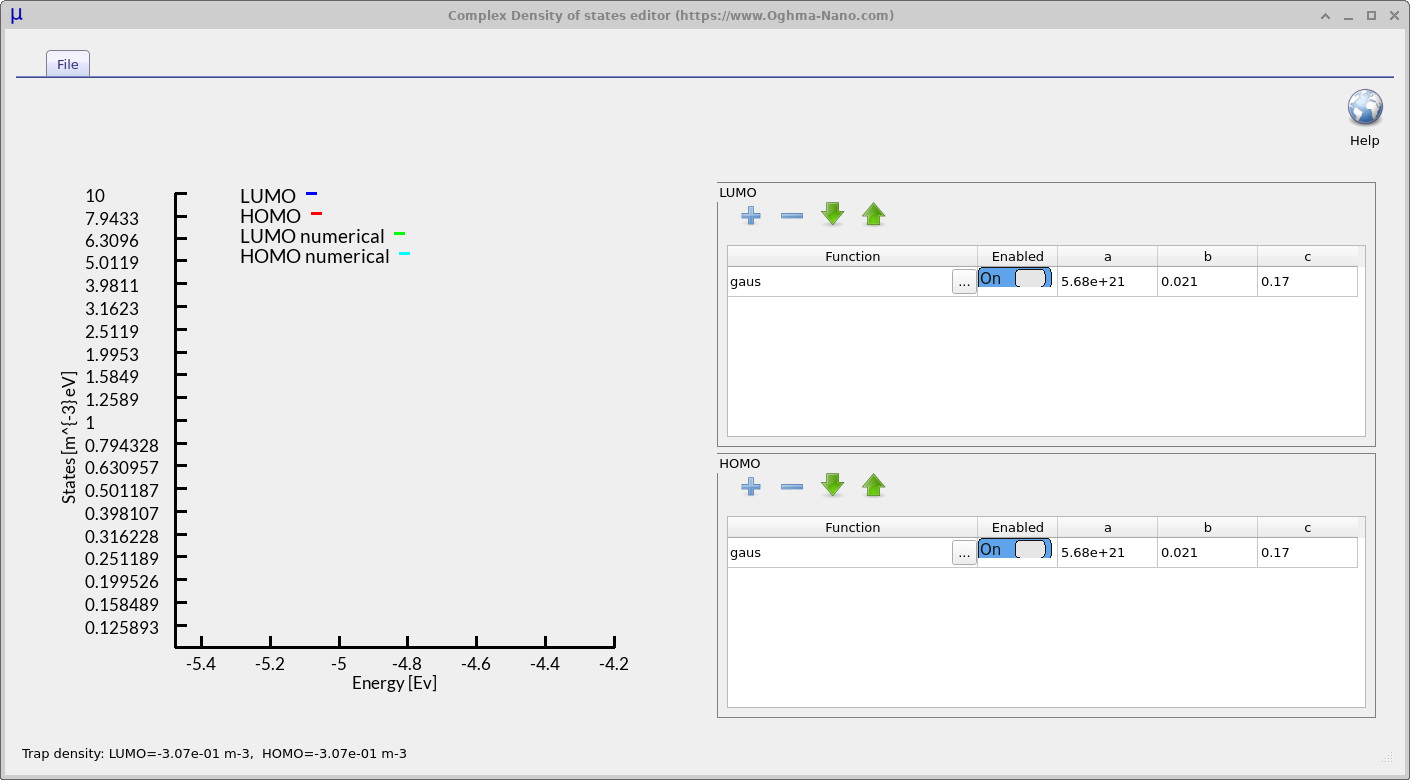
5. More Complex Distributions of States

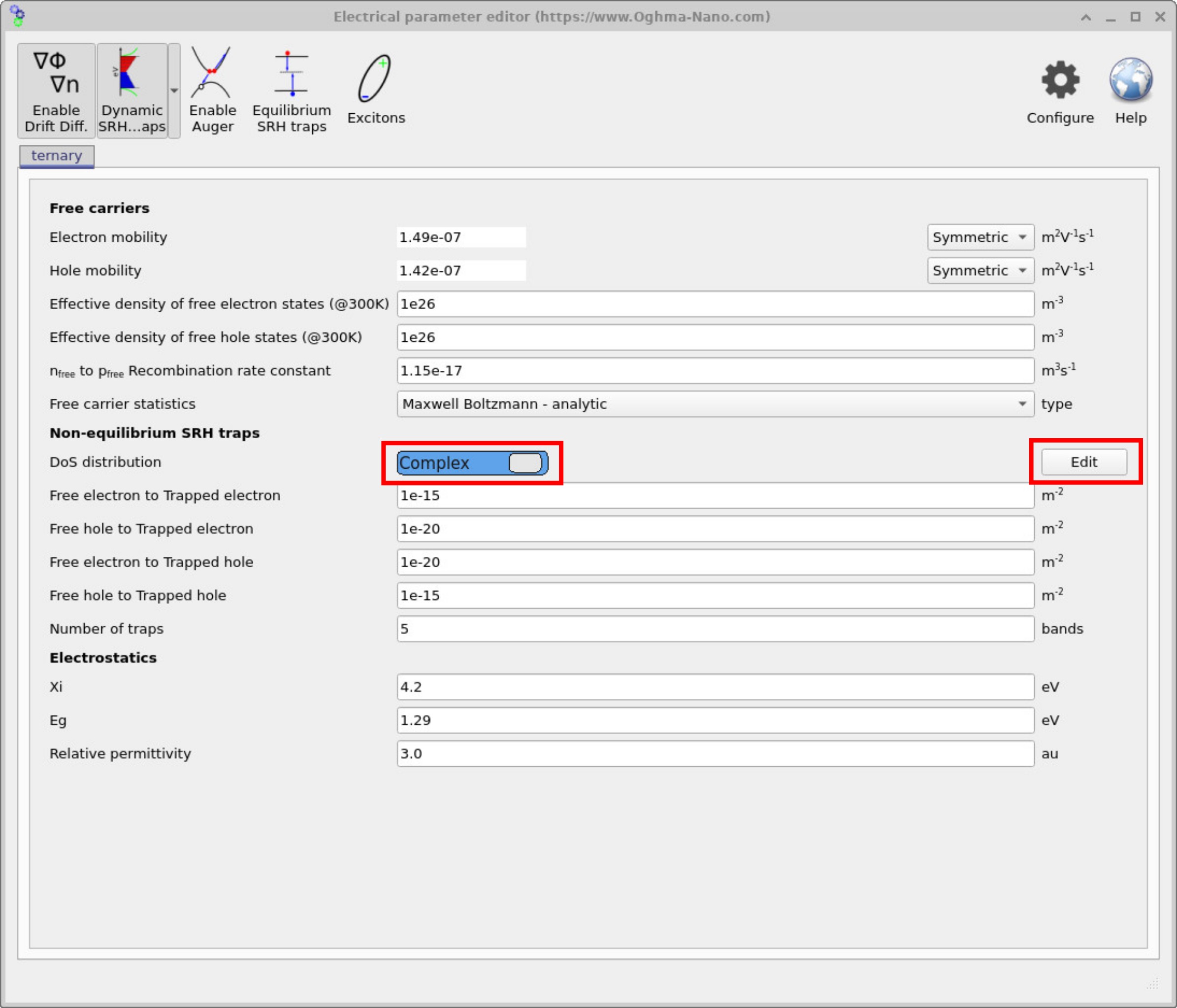
By default, the dynamic Shockley–Read–Hall (SRH) model assumes an exponential distribution of trap states. However, experimental studies have shown that the density of states (DoS) in disordered semiconductors is often not purely exponential. In some reports, the distribution is closer to Gaussian; in others, it is best described as a mixture of Gaussian and exponential components; and in more complex cases, entirely different functional forms are required. In all situations, the exact shape of the DoS is strongly dependent on the energetic position of the states within the bandgap.

Figure 8 shows the electrical parameters available for defining the DoS of a Shockley–Read–Hall trap distribution. If the DoS type is switched from Exponential to Complex and the Edit button is clicked, the interface shown in Figure ?? appears. Here, users can define arbitrary energetic distributions of trap states, including Gaussian, exponential, Lorentzian, or combinations of these functions.