Organic Solar Cell (OPV) Tutorial – Part D: Parasitic Components & Dark JV

1. Parasitic components and the JV curve

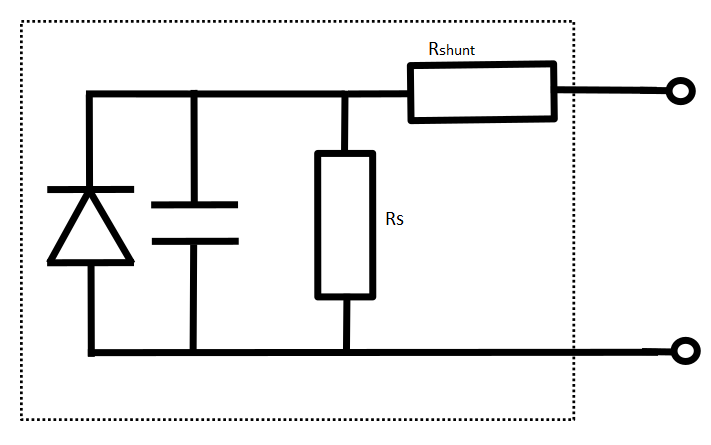
Drift–diffusion simulations describe the photoactive layer in detail, where electrons and holes are both present and interact. Real devices, however, also include non-ideal effects introduced by the contact layers and fabrication imperfections. One important effect is the series resistance (R_s), a lumped resistance in series with the diode that arises from contacts, transport layers (HTL/ETL), and wiring or sheet resistance. It produces the characteristic high-bias “roll-off,” limiting the current at large forward voltages and reducing the fill factor.

A second effect is the shunt resistance (R_shunt), a leakage path in parallel with the active layer. This is caused by imperfections such as pinholes, impurities, edge leakage, or micro-shorts that create unintended conductive pathways through the device. It mainly degrades the low-bias region of the JV curve, reducing the slope near the origin and lowering J_SC and fill factor.

These contributions are usually referred to as parasitic components and can be represented in a compact circuit model, shown in ??. In this model, the ideal diode (governed by the drift–diffusion equations) appears in parallel with R_shunt and in series with R_s. A parasitic capacitor is also included to represent the geometric capacitance of the contacts; this term is only relevant in transient simulations.

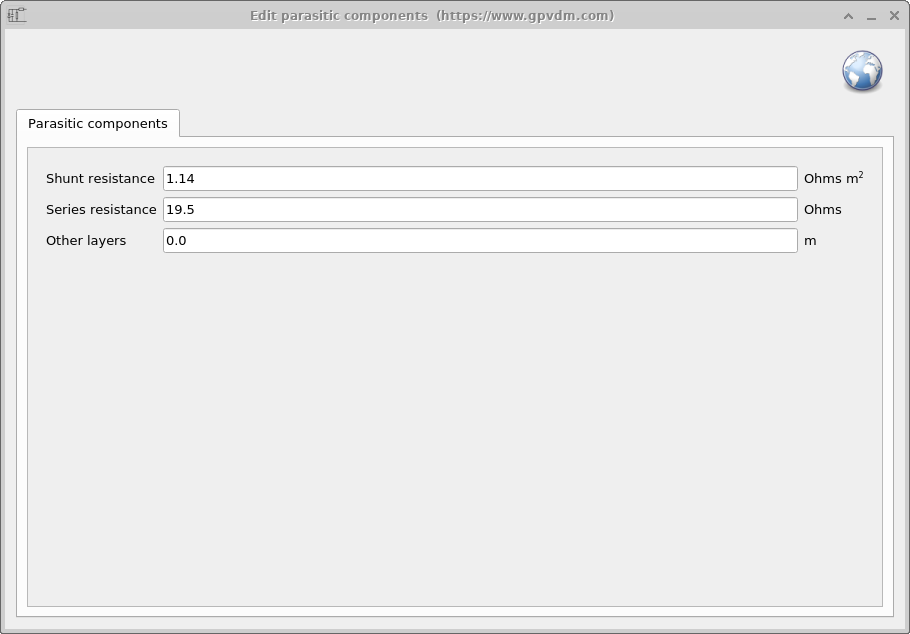
You can edit parasitic components in OghmaNano by going to the Electrical ribbon in the main window and selecting Parasitic components. This opens the Parasitic component editor, where you can set both the shunt and series resistances. This can be seen in ?? Shunt resistance (R_shunt) is entered as an area-normalised value (Ω·m²). This ensures that the effective shunt resistance scales with device area. Series resistance (R_s) is specified in ohms (&Omega) as a lumped resistance, independent of device area. Together, R_shunt and R_s allow you to capture real-world leakage and conduction losses in addition to the drift–diffusion physics of the active layer.

2. Solar cells in the dark

Up to now, all simulations have been run in the light under AM1.5G illumination. This is natural, since we are usually interested in how much power a solar cell can generate. However, measuring a device in the dark often reveals even more about its internal physics — and why it may not be performing as expected. A common mistake is to characterise a new device only under illumination; in fact, the dark JV curve can provide richer diagnostic information than the light curve.

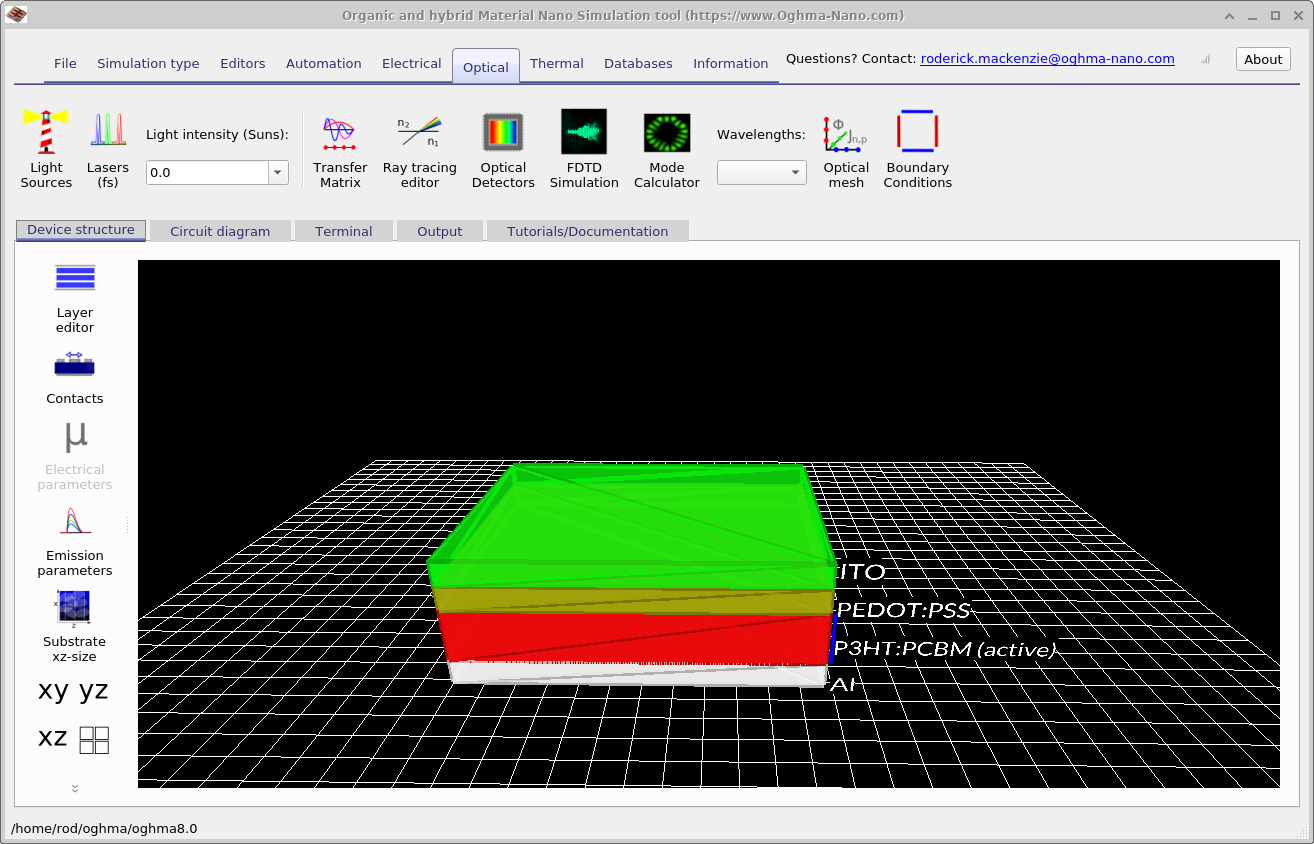
In this section we will use the dark JV to investigate how R_shunt and R_s can be extracted. To begin, switch the simulator into darkness: go to Optical ribbon → Light intensity (suns) and set the value to 0.0. The green photons in the 3D device view will disappear, confirming that the simulation is running without illumination. This can be seen in ??.

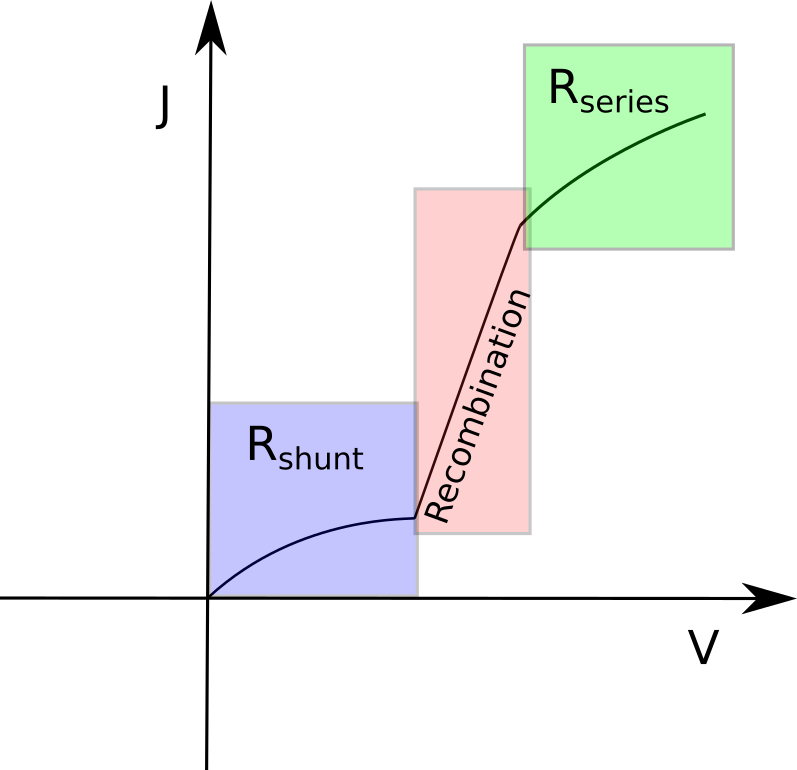
Next we will explore how parasitic resistances shape the dark JV. Start by setting R_shunt to a high value (e.g. 1 MΩ·m²) and run a JV sweep, then reduce it to a much lower value (e.g. 1 Ω·m²) and compare the curves. Observe how the slope at low voltages is affected by shunt leakage. Then repeat the process for the series resistance: set R_s first to 0 Ω, then to a larger value (e.g. 20 Ω). Compare the high-voltage region of the JV and note how the roll-offchange. Plot each case on x-linear / y-log axes (press l) so the differences are clearly visible. ?? plots how the resistances should affect the different parts of the JV curve. Note by changing only the resistances we can not affect the recombination region - this comes later.