有机器件模型中陷阱态的必要性

本节解释了为何在模拟聚合物:富勒烯共混物、小分子体系或非晶半导体等无序材料时必须考虑陷阱态。若不对俘获与释放进行显式处理，任何器件模型都无法捕捉电荷输运与复合的物理过程。因此，使用完整的 Shockley–Read–Hall（SRH）复合与俘获形式主义对于获得具有物理意义的结果是必不可少的。

关键要点：为什么必须包含陷阱态：

如果忽略陷阱态，费米能级–电子密度关系将是错误的。
费米能级依赖关系不正确意味着复合随电压的变化也会错误。
迁移率随电压的关系同样会被错误表征。
因此，你无法用具有物理意义的参数复现实验的J–V 曲线。

关键结论：确保正确的载流子–费米能级依赖关系至关重要；否则，器件仿真将无法捕捉真实的物理行为。

1. 无序材料的物理与能量结构

传统的无机半导体（如晶体 Si 或 GaAs）既高度有序又极其纯净—— 常可达到“九个九”的纯度（99.9999999%）。相比之下，有机半导体的纯度很少超过 99.9%，这使其缺陷含量约比无机材料高一百万倍。在结构上差异同样显著：无机半导体形成规则的晶格，类似于弹珠在棋盘上整齐排列 (??)。硅本身采用金刚石立方结构，是近乎完美的晶格 (??)。相比之下，有机材料是“柔软”的分子体系，缠结的聚合物类似一盘意大利肉酱面—— 面条代表聚合物链，酱汁代表小分子 (??)。有机共混物的模拟证实了这一图景，显示出类似意大利面条的聚合物堆积，并夹杂富勒烯衍生物 (??)。

Marbles arranged neatly on a board, illustrating an ordered structure. — 弹珠按规则网格排列——类比一个完全有序的结构。

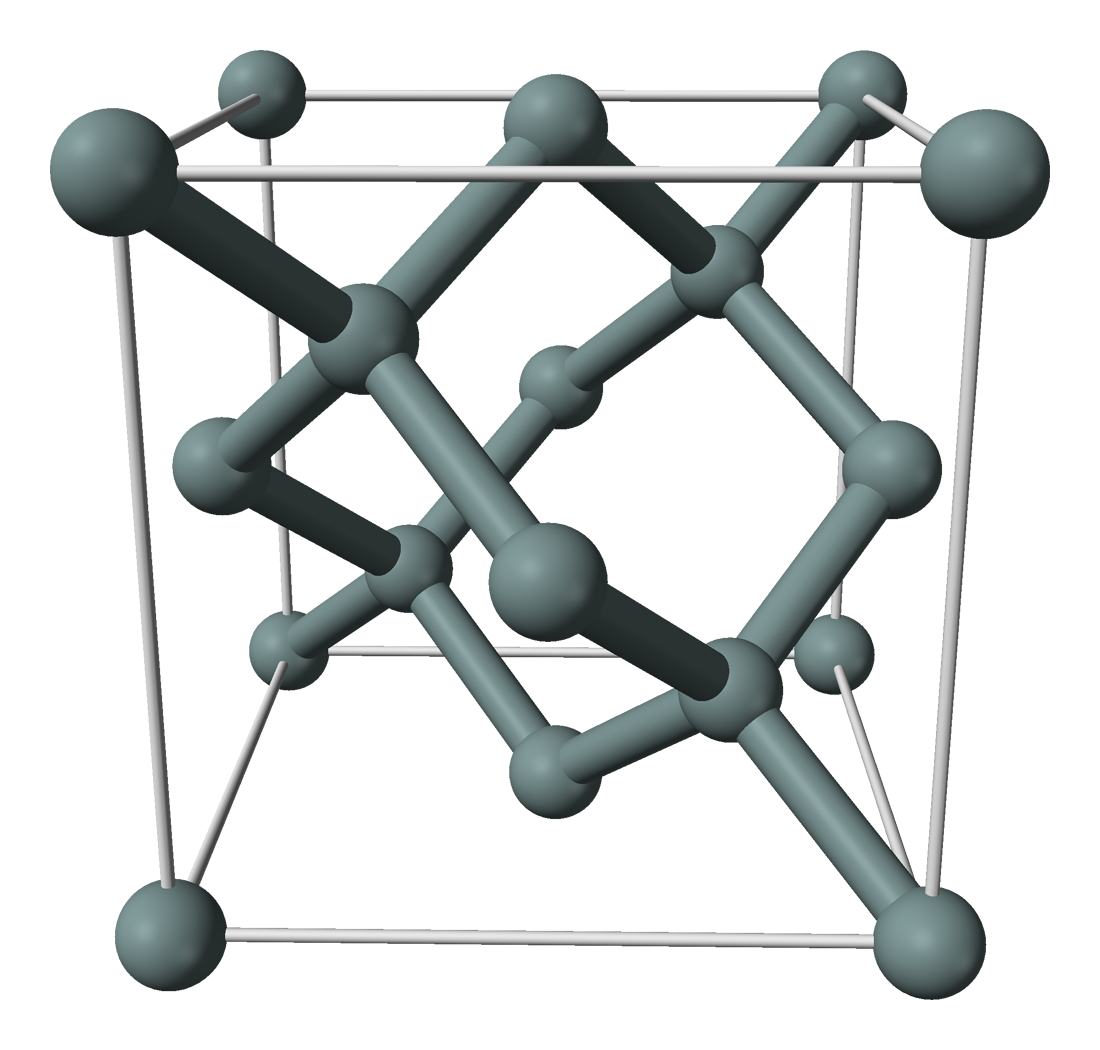
Atomic structure of crystalline silicon showing a diamond lattice. — 具有金刚石晶格的晶体硅——高度有序材料的例子。

A plate of tangled spaghetti, illustrating disorder. — 一盘意大利面——这里用作高度无序体系的类比。

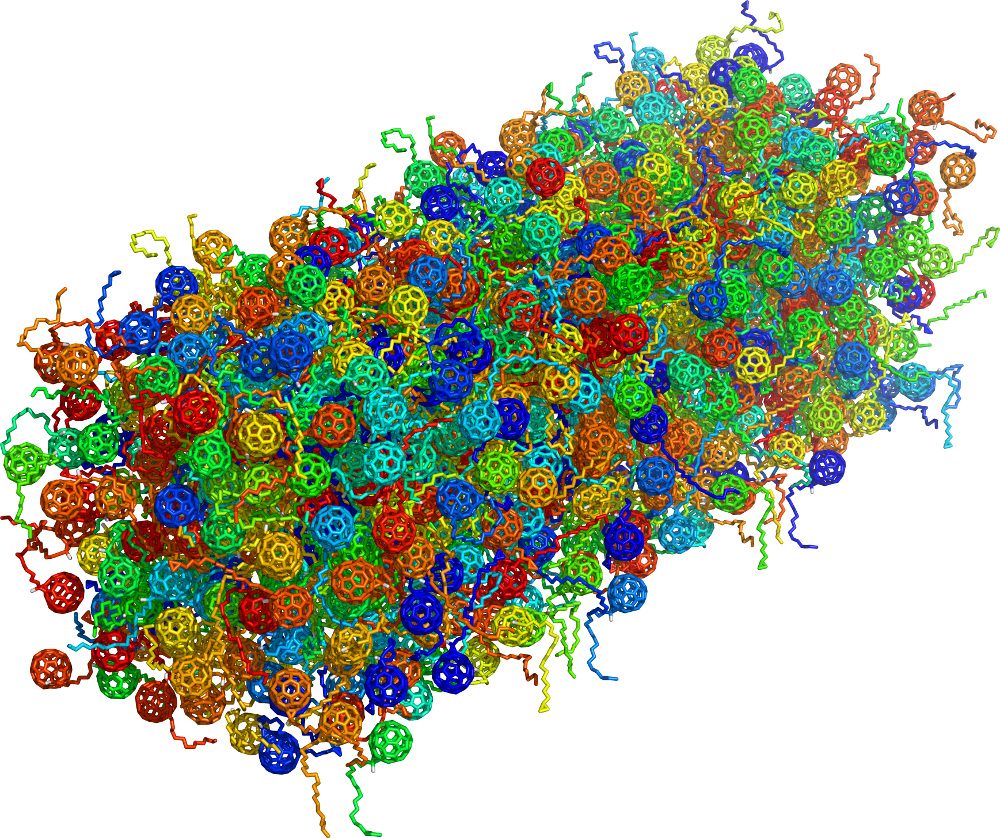
Simulation of organic polymers packed in a disordered spaghetti-like morphology. — 模拟得到的无序有机聚合物共混物——与上面的意大利面类比相当。

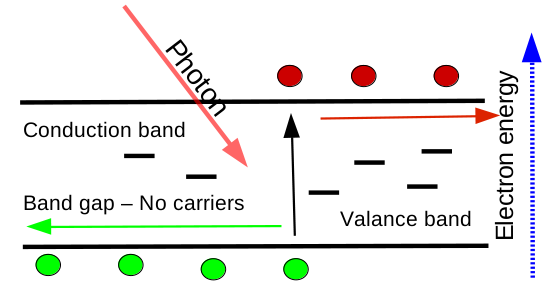
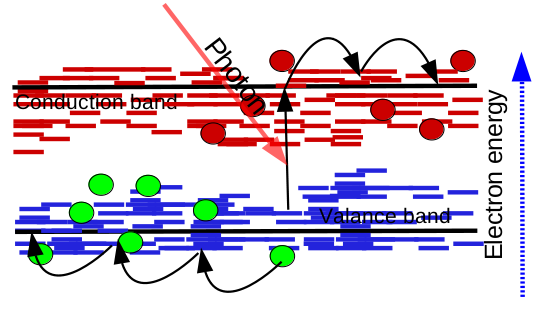
这些结构差异导致了截然不同的能量景观。在晶体半导体中，电子与空穴在明确的导带与价带中自由移动，在外加电场下只经历较小的阻碍。这种带输运如 ?? 所示。而在无序有机半导体中，杂质与结构无序会在带隙中引入密集分布的局域陷阱态。载流子不再通过延展态自由传播，而必须在陷阱之间进行热激发跳跃。这种陷阱主导的输运在 ?? 中作了示意。

结论很清楚：在有序半导体中陷阱态往往可以忽略，但在无序体系中它们主导物理过程。因此，任何现实的器件模型都必须包含对陷阱分布与 Shockley–Read–Hall 动力学的详细描述。OghmaNano 正是如此，使得能够以物理精度模拟无序体系，如有机太阳能电池、OFETs 与钙钛矿等。

为了说明其重要性，我们现在转向载流子密度与费米能级之间的关系，并考察一些具体示例。

关键要点：

有序半导体（例如 Si、GaAs）极其纯净且为晶体结构，因此载流子在带态中自由移动。
无序半导体（例如有机、钙钛矿）杂质多且结构混乱，因此输运由陷阱态与跳跃主导。

Band structure of an ordered semiconductor such as silicon or GaAs, showing well-defined conduction and valence bands with minimal trap states. Carriers move primarily by ballistic or drift-diffusion transport. — (a) **有序半导体**（如硅或 GaAs）的能带结构。陷阱态很少时，载流子可在导带或价带中高效移动，主要通过弹道或漂移-扩散输运。

Band structure of a disordered semiconductor such as an organic blend (e.g. PM6:Y6 or P3HT:PCBM), showing many localized trap states within the band gap. Carriers move by hopping transport between localized states. — (b) **无序半导体**（如 PM6:Y6 或 P3HT:PCBM）的能带结构。带隙内存在多个局域陷阱态，电荷输运通过在这些态之间跳跃实现，而非自由带输运。

2. 为什么陷阱态对器件建模很重要（无数学）

有机及其他无序半导体的一个核心特征是：载流子密度是外加电压与光照强度的强函数。随着偏压或光强增加，更多电荷被注入或光生进入器件。由于这些材料在带隙中具有大量陷阱态，载流子会先填充这些陷阱，然后才占据延展态。陷阱填充意味着即便电压的微小变化也可能引起自由载流子密度的巨大变化。

这之所以重要，是因为器件中的复合直接依赖于载流子密度。复合速率的一般形式为

\[ R = k_r \, n(V)\, p(V), \]

其中 \(k_r\) 为复合常数，\(n(V)\) 与 \(p(V)\) 为随电压变化的电子与空穴密度。如果由于忽略陷阱态而使 \(n(V)\)（以及 \(p(V)\)）的函数形式错误，那么复合速率也会错误。这将直接导致对开路电压（\(V_{OC}\)）及其他关键器件特性的错误预测。

迁移率同样会受到影响。在无序体系中，有效载流子迁移率取决于自由载流子与俘获载流子的平衡。一个简单表达式为

\[ \mu_e(n) = \frac{\mu_e^0 \, n_{\text{free}}}{n_{\text{free}} + n_{\text{trap}}}, \]

其中 \(\mu_e^0\) 为本征电子迁移率，\(n_{\text{free}}\) 为可移动载流子密度，\(n_{\text{trap}}\) 为被俘获载流子密度。如果密度–电压关系错误，那么预测的迁移率–电压依赖也会错误。综合这些误差，即便复合或迁移率参数在其他方面合理，模拟得到的 J–V 曲线也无法与实验匹配。

关键要点：

若忽略陷阱态，载流子密度随电压的关系将是错误的，从而导致错误的复合速率与 \(V_{OC}\)。
有效迁移率取决于自由与俘获载流子的平衡，因此忽略陷阱也会给出错误的迁移率–电压依赖与 J–V 曲线。

3. 为什么陷阱态对器件建模很重要（含数学）

为了正确描述载流子密度，必须考虑底层的态密度（DoS）。图 ?? 示意了前面 ?? 与 ?? 所示有序与无序能带结构对应的 DoS。在有序半导体中，DoS 具有尖锐的带边（抛物带），费米–狄拉克占据位于导带边之上。然而在无序半导体中，DoS 显示出延伸到带隙深处的局域陷阱态尾部（常用指数或高斯尾来建模）。其结果是两种情况下载流子占据的分布在本质上不同。

Left: Ordered semiconductor, carriers populate states above a sharp conduction-band edge. Right: Disordered semiconductor, carriers occupy a broad distribution of localized trap states extending into the band gap. — 有序与无序材料中的载流子统计。有序材料具有尖锐的带边且载流子处于延展态；无序材料存在带隙尾态，载流子被俘获在带隙深处。

形式上，总电子密度由 DoS 与费米–狄拉克占据加权积分给出：

\[ n(E_f,T) = \int_{E_{\min}}^{\infty} \rho(E)\, f(E,E_f,T)\, dE, \]

其中 \(E_f\) 为准费米能级，\(\rho(E)\) 为 DoS，\(f(E,E_f,T)\) 为费米–狄拉克分布。在有序材料中，\(\rho(E)\) 很尖锐，因此只有导带边以上的态贡献。在无序材料中，\(\rho(E)\) 包含大量陷阱尾态，因此载流子可存储在接近费米能级的位置，在相同偏压下产生比有序晶体高一到两个数量级的电荷密度。这在电荷抽取实验中可直接观察到。

结论很直接：正确获得载流子密度的依赖关系并非可选项。没有陷阱态模型，复合与迁移率作为电压函数都会错误，且无法复现实验中真实的 J–V 曲线。OghmaNano 显式包含这些陷阱态，使得能够对 PM6:Y6 与 P3HT:PCBM 共混物等无序器件进行准确建模，同时在关闭陷阱时也可模拟更有序的半导体。

关键要点：

在有序半导体中，载流子主要占据尖锐带边以上的延展态。
在无序半导体中，陷阱尾态主导，载流子存储在带隙深处。
若不在 DoS 中包含陷阱态，载流子密度随电压的关系将错误，从而导致错误的复合、迁移率与 J–V 曲线。

4. 为什么不应在器件模型中使用 Langevin 复合

经典 Langevin 复合速率定义为

\[ R_{\text{free}} = q \, k_r \, \frac{\mu_e + \mu_h}{2 \, \epsilon_0 \epsilon_r} \, n p , \]

其中 \(R_{\text{free}}\) 为复合速率，\(k_r\) 为经验的 Langevin 缩减因子， \(\mu_e\) 与 \(\mu_h\) 为电子与空穴迁移率，\(n\) 与 \(p\) 为载流子密度， \(\epsilon_0 \epsilon_r\) 为介电常数。乍看之下这似乎合理：假定当电子与空穴在布朗运动下足够接近并感受到库仑场时就会发生复合。这一图景适用于在简单液体或离子导体中完全自由的载流子。但在有机光伏（OPV）与其他无序半导体中，Langevin 模型背后的假设会失效。

为什么会失效？ 实验研究——尤其是 2010 年代初期的工作——很快表明，Langevin 复合无法自洽地同时再现暗态与受光的 J–V 曲线。该模型系统性地高估复合速率，常常高出数个数量级。为了使拟合可行，研究者引入了“Langevin 缩减因子” \(k_r\)，有时小到 10⁻³。虽然方便，但这一调整实际上承认了该机制在这些体系中并不成立。

当我们更仔细地审视该方程时，问题就很清楚了：

载流子密度依赖错误。 速率严格按 \(np\)（二阶）缩放。在实验中，OPV 的复合往往遵循如 \((np)^{1.5}\) 之类的非整数幂律，反映了陷阱限制动力学与局域态分布。Langevin 形式根本无法捕捉这一点。
对迁移率的处理不正确。 方程假设固定迁移率 \(\mu_e\) 与 \(\mu_h\)。实际上，无序半导体中的迁移率强烈依赖于载流子密度（见上文讨论）。将错误的迁移率依赖代入会进一步扭曲预测的复合速率。
忽略陷阱与无序。 Langevin 机制将所有载流子都视为自由载流子。在 OPV 等材料中，多数载流子会在局域态中被俘获并仅间歇性地参与导电。因此复合取决于陷阱景观，而不仅仅是自由载流子的运动。

综合这些问题，Langevin 复合至多是粗糙近似，最坏情况下会产生误导。即便拟合得到缩减因子 \(k_r\)，它也无法捕捉陷阱辅助复合与迁移率随电压变化的正确物理。在器件模型中使用 Langevin 复合因此就像把方钉硬塞进圆孔：它也许能给出一个数，但不会给出具有物理意义的结果。

Langevin 复合的关键要点

Langevin 复合在 OPV 与无序半导体中系统性地高估复合速率。
它假设所有载流子都是自由的且迁移率固定——忽略陷阱与载流子密度依赖。
历史上引入缩减因子（\(k_r\)）以强行拟合，但这凸显了该模型的无效性。
准确建模需要陷阱辅助复合机制（例如 Shockley–Read–Hall），而不是 Langevin。

5. 如何让 Langevin 复合在器件模型中“可用”

经典 Langevin 复合的关键问题在于其对载流子密度的依赖不正确，并且需要任意的缩减因子。研究者尝试让 Langevin 复合“可用”的一种方式，是在迁移率本身引入载流子密度依赖，例如：

\[ R_{\text{free}} = q \, k_r \, \frac{\alpha \mu_e(n) + \beta \mu_h(n)}{2 \, \epsilon_0 \epsilon_r} \, n_{\text{tot}} p_{\text{tot}} , \]

在这里定义一个迁移率边：迁移率边以上的载流子参与导电，而以下的载流子被视为被俘获。平均迁移率可表示为

\[ \mu_e(n) = \frac{\mu_e^0 \, n_{\text{free}}}{n_{\text{free}} + n_{\text{trap}}}, \qquad \mu_h(p) = \frac{\mu_h^0 \, p_{\text{free}}}{p_{\text{free}} + p_{\text{trap}}}. \]

如果自由载流子密度远小于俘获载流子密度，则可得到有效复合速率

\[ R(n,p) = q \, k_r \, \frac{\alpha \mu_e^0 \, n_{\text{free}} p_{\text{trap}} + \beta \mu_h^0 \, p_{\text{free}} n_{\text{trap}}} {2 \, \epsilon_0 \epsilon_r}. \]

这样，Langevin 复合就被有效地重新解释为自由与俘获载流子之间的相互作用（\(n_{\text{free}}p_{\text{trap}}\) 与 \(p_{\text{free}}n_{\text{trap}}\)）。这在本质上等价于 Shockley–Read–Hall（SRH）复合图景：自由载流子与被俘获载流子发生复合。

该方法在稳态下表现尚可，但它依赖一个强假设：在给定位置所有载流子共享单一准费米能级，即它们处于局部平衡并具有无限的热化速度。这在稳态条件下或许可行，因为载流子有时间达到平衡，但在时域中会失效。实际上，有机半导体中密集的陷阱态分布使得载流子不太可能像一个单一平衡气体那样行为。相比之下，SRH 形式主义避免了这一假设，因此对无序材料中的复合与俘获提供了更符合物理的描述。

总体要点：

陷阱态主导无序半导体中的电荷输运与复合。
准确的载流子密度随电压的依赖关系对于现实建模至关重要。
对陷阱的错误处理会导致错误的复合、迁移率与 JV 曲线。
OghmaNano 包含完整的陷阱态与 SRH 处理，从而实现具有物理意义的器件仿真。