使用 Shockley-Read-Hall 陷阱态的非平衡载流子俘获与复合
1. 简介
许多读者第一次接触 Shockley–Read–Hall(SRH)复合,可能是在本科物理课程中。 它通常被介绍为自由载流子与被俘获载流子之间的一种复合机制,并可用下述广为人知且简化的表达式概括:
\[R_{\mathrm{SRH}} = \frac{np - n_{i}^{2}} {\tau_{p}(n + n_{1}) + \tau_{n}(p + p_{1})} \]
其中:
- \(\tau_{n}\)、\(\tau_{p}\) 为与陷阱相关的电子与空穴寿命,
- \(n_{1} = N_{C} \exp\!\big(-(E_{C} - E_{t})/k_{B}T\big)\) 为当陷阱处于平衡时的有效电子密度,
- \(p_{1} = N_{V} \exp\!\big(-(E_{t} - E_{V})/k_{B}T\big)\) 为相应的空穴密度,
- \(E_{t}\) 为陷阱能级,\(n_{i}\) 为本征载流子浓度。
该方程最初由 Shockley & Read, Physical Review 87, 835 (1952) 推导得到,并在手册的 SRH 理论章节 中进行了更详细的描述。
然而,需要注意的是,上述方程并非全部内容。 这一紧凑形式源自原始 Shockley–Read–Hall 分析在一组简化假设下得到的结果:
- 稳态条件:假定陷阱占据数不随时间变化,因此俘获与发射速率相互平衡。
- 单一陷阱能级:复合通过带隙内能量为 \(E_t\) 的单一、能量上很尖锐的缺陷能级发生。
这些假设在仅含少量杂质的材料中完全足够,在这种情况下陷阱辅助复合仅起到较小作用,单一离散陷阱能级能够给出合理描述。然而,一旦 Shockley–Read–Hall 复合成为主导过程(这在无序半导体中经常发生),图景就会改变。在这类体系中,陷阱很少集中在单一能量处,而是形成带隙内的宽能量分布,因此用态密度描述更为合适。此外,大量被占据的陷阱会引入显著的俘获电荷,这些电荷不仅作为复合通道,还作为载流子库,重塑器件中的静电势分布。这意味着陷阱占据必须与泊松方程自洽处理,而不能作为被动背景过程。此外,稳态假设阻止了对动态过程的描述:在时间分辨实验或瞬态仿真中,陷阱占据会随时间演化,而这种演化本身对复合动力学至关重要。因此,尽管紧凑的 SRH 公式是一个很好的起点,但在高陷阱密度材料或非平衡动力学重要的情形下必须加以推广。
为了正确理解并考虑稳态 Shockley–Read–Hall 形式与原始工作中更一般处理之间的差异,我们需要更深入地探讨其基础理论。
2. 理解动态 SRH 速率方程
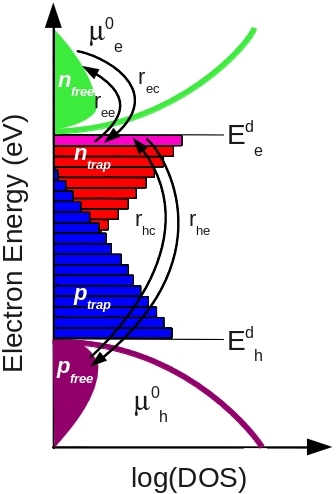
要真正理解 Shockley–Read–Hall(SRH)形式主义的含义,我们需要仔细观察原作者是如何建立该理论的。 他们所做的是为半导体带隙内陷阱态的占据写出一个 速率方程。 该速率方程如下所示,并在 ?? 中以示意方式展示。 它描述了由于俘获与逃逸过程导致陷阱中载流子数目的变化。
\[ \frac{dn_t}{dt} = r_{ec} - r_{ee} - r_{hc} + r_{he} \]
在该表达式中,四项分别对应与电子陷阱相关的四种可能载流子流。 \(r_{ec}\) 表示从自由电子群体进入陷阱的 电子俘获, 而 \(r_{ee}\) 表示返回自由能带的 电子发射。 类似地,\(r_{hc}\) 是进入陷阱的 空穴俘获 速率, \(r_{he}\) 是返回自由空穴群体的 空穴发射 速率。 这些过程共同描述了单一陷阱能级中载流子流入与流出的细致平衡。
将这些贡献在概念上加以区分是有帮助的。 电子俘获与发射项(\(r_{ec}\)、\(r_{ee}\))描述纯粹的 电荷俘获, 这与人们通常对陷阱存储电子的理解一致。 空穴俘获与发射项(\(r_{hc}\)、\(r_{he}\))描述 复合, 因为它们表示与自由空穴群体相互作用导致俘获电荷的湮灭或再生。 这里的关键点在于:陷阱本身确实包含电荷——它并非仅是一个用于复合的数学“汇”,而是一个真实的载流子库, 在对复合与器件静电学进行建模时都必须加以考虑。
2. 逃逸 vs. 俘获概率
载流子与陷阱相互作用的俘获与逃逸速率汇总在 下表 中,而相应的逃逸概率给出在其后的方程中。 Shockley–Read–Hall 理论的一个关键特征是逃逸概率对陷阱能量深度的强依赖性。 靠近带边的陷阱中被俘获的载流子较容易逃逸,而更深陷阱中的载流子发射概率要低得多。 这种行为直接反映在逃逸概率表达式的指数项中。 相比之下,载流子被俘获进陷阱的概率并不依赖陷阱深度;它只取决于陷阱是空的还是被占据。 空陷阱很可能俘获接近的载流子,而完全占据的陷阱无法俘获额外载流子。 纵览 表 9.1,可以看到这些原则在俘获与逃逸速率中以数学形式体现出来。 它们共同描述了这样一个系统:载流子容易落入陷阱;若陷阱在能量上更深,则越来越难以逃逸;并且电子与空穴都可能被俘获。 一旦两种载流子占据同一陷阱,复合便自然发生。
| 机制 | 符号 | 表达式 |
|---|---|---|
| 电子俘获速率 | \(r_{ec}\) | \(n v_{th} \sigma_{n} N_{t} (1-f)\) |
| 电子逃逸速率 | \(r_{ee}\) | \(e_{n} N_{t} f\) |
| 空穴俘获速率 | \(r_{hc}\) | \(p v_{th} \sigma_{p} N_{t} f\) |
| 空穴逃逸速率 | \(r_{he}\) | \(e_{p} N_{t} (1-f)\) |
逃逸概率由下式给出:
\[\label{eq:taile} e_n=v_{th}\sigma_{n} N_{c} exp \left ( \frac{E_t-E_c}{kT}\right )\]
以及
\[ e_p = v_{th} \sigma_{p} N_{v} \exp\!\left( \frac{E_{v} - E_{t}}{kT} \right) \]
占据函数由下式给出,\[f(E_{t},F_{t})=\frac{1}{e^{\frac{E_{t}-F_{t}}{kT}}+1}\] 其中,\(E_{t}\) 为陷阱能级,\(F_{t}\) 为陷阱的费米能级。
3. 从单一陷阱到 DoS
到目前为止,如 图 9.1 所示,我们考虑的是单一陷阱能级(“紫色陷阱”)的行为。 然而,在真实的无序半导体中,复合很少由单一离散态主导。 相反,存在从导带与价带边缘向带隙内延伸的 陷阱能级分布。 这意味着我们不仅需要描述电子陷阱,还需要描述空穴陷阱,以及它们各自随能量变化的密度。
为此,陷阱密度用态密度函数 \(\rho(E)\) 描述,它可以设置为与所研究材料相适应的任意解析形式。 在此示例中,我们采用指数分布的陷阱态:
\[ \rho^{e/h}(E) = N^{e/h} \exp\!\left( \frac{E}{E_{u}^{e/h}} \right), \]
其中 \(N^{e/h}\) 为带边(LUMO 或 HOMO)处的态密度,单位为每 eV 的态数, \(E_{u}^{e/h}\) 为定义指数尾部的特征斜率能量。 与特定能级相关的有效陷阱密度可通过对表示该陷阱的能量区间 \(\Delta E\) 进行平均而得到:
\[ N_{t}(E) = \frac{ \int_{E - \Delta E / 2}^{E + \Delta E / 2} \rho^{e}(E)\, dE }{ \Delta E }. \]
在实际中,模型将该分布离散为有限数量的陷阱能级。 对于每一个陷阱能级,我们如前所述写出一条独立的速率方程,并为其分配相应的密度 \(N_t\)。 通常在导带与价带下方各使用三到二十个陷阱能级,每个都可以存储电荷。 随后,总的俘获电荷与泊松方程自洽耦合,确保器件的静电分布能够反映陷阱占据情况。
最后,陷阱辅助复合项会在载流子连续性方程中显式出现。例如, Shockley–Read–Hall 复合速率可写为
\[ R_{\mathrm{SRH}} = r_{hc} - r_{he} \;=\; r_{ec} - r_{ee}, \]
从而将电子与空穴的俘获与逃逸速率直接与导带与价带中载流子平衡联系起来。 通过这种方式,俘获与复合过程被平等描述,并且它们的贡献被自然地整合进 支配器件运行的连续性方程与泊松方程之中。
最终结果
在能量空间与位置空间中跨器件求解完整的 Shockley–Read–Hall 方程组的结果是, 我们能够不仅从位置角度,而且从能量角度描述电荷的分布位置。 这使我们能够捕捉在高度无序材料中占主导地位的电荷动力学。 如 ?? 所示,我们在暗态条件下仿真一条 J–V 曲线, 施加偏压从 0 V 增加。随着偏压上升,载流子从电极注入并逐步填充陷阱态。 这些俘获电荷同时作为复合中心以及空间电荷源,重塑器件中的静电势分布。 若不包含这些效应,任何器件仿真都将是不完整且很可能是错误的。 关于为何必须在此类模型中包含陷阱态的详细讨论,请参见 本节。
👉 下一步:现在继续阅读 解析稳态 SRH 复合