Shockley–Read–Hall（SRH）复合模型

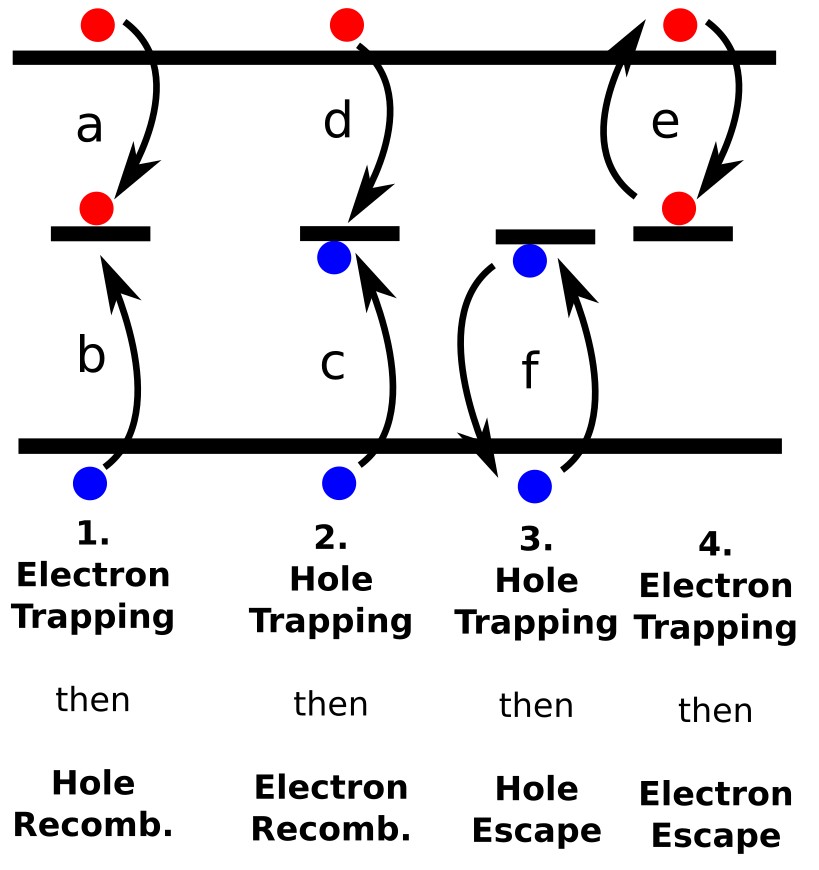
Shockley–Read–Hall（SRH）复合描述了通过带隙内局域缺陷态 （陷阱）引起的载流子损失过程。这是一种陷阱辅助机制：电子（或空穴）首先被俘获 到缺陷态中，随后要么与相反类型的载流子发生复合，要么通过 热激发重新释放。?? 示意了单一带隙中部陷阱态的四种主要路径，跃迁标记为（a–f）：

• 1. 电子俘获：电子被俘获（a），随后与被俘获的空穴发生复合（b）。
• 2. 空穴俘获：空穴被俘获（d），随后与被俘获的电子发生复合（c）。
• 3. 伴随逃逸的空穴俘获：空穴被俘获，随后发生热再发射（f）。
• 4. 伴随逃逸的电子俘获：电子被俘获，随后发生热再发射（e）。

这些过程表明，同一陷阱既可以介导复合，也可以介导载流子释放。 SRH 复合本质上是一个两阶段机制：首先载流子被俘获 （a、d），只有在随后相反载流子被俘获时才发生复合（b、c）。 如果没有相反载流子到达，被俘获的载流子可能通过热激发逃逸（e、f）。 SRH 复合的总体效率取决于陷阱密度、陷阱在带隙中的能级位置、 载流子俘获截面以及被俘获载流子的相对寿命。

标准 SRH 复合速率

在 SRH 模型下，陷阱辅助复合的净速率为：

\[R_{\mathrm{SRH}} = \frac{np - n_{i}^{2}} {\tau_{p}(n + n_{1}) + \tau_{n}(p + p_{1})} \]

其中：

• \(\tau_{n}\)、\(\tau_{p}\) 为与该陷阱相关的电子与空穴寿命，
• \(n_{1} = N_{C} \exp\!\big(-(E_{C} - E_{t})/k_{B}T\big)\) 为陷阱处于平衡时的有效电子密度，
• \(p_{1} = N_{V} \exp\!\big(-(E_{t} - E_{V})/k_{B}T\big)\) 为对应的空穴密度，
• \(E_{t}\) 为陷阱能级，\(n_{i}\) 为本征载流子浓度。

在该表述中，复合过程以单一陷阱能级来描述。 因此，SRH 模型被广泛采用，因为它给出了一个 易于计算的解析表达式，并捕捉了缺陷态在复合中的核心作用。

标准 SRH 模型的局限性

尽管功能强大，标准 SRH 方程仍存在若干重要局限：

• 单能级近似 —— 仅考虑一个离散的陷阱能级， 而真实半导体（尤其是有机和无序体系）通常包含 宽分布的陷阱态。
• 无显式静电学 —— 该模型将陷阱仅视为复合中心。 暂时被俘获在陷阱中的电荷并未纳入器件的静电势计算， 因此忽略了其对空间电荷和内部电场的影响。
• 仅关注复合 —— 该表达式未显式描述俘获与去俘获动力学， 而仅以其净效应体现为复合。

为克服这些局限，必须在 陷阱态分布上显式求解 SRH 形式， 从而能够正确表征复合速率以及陷阱占据情况 （进而包括其静电贡献）。 这种更一般的处理方法在 此处 进行了描述。

在 OghmaNano 中，标准 SRH 复合项可以在 电学参数编辑器中启用或禁用， 并且寿命参数 \(\tau_{n}\) 与 \(\tau_{p}\) 可由用户指定。

在 OghmaNano 中使用 SRH